Математика. Часть 4 (Вычислительная математика): План-конспект лекционного курса, страница 18

К сожалению, метод золотого сечения неустойчив к ошибкам в определении числа , поэтому существуют различные модификации этого
метода, а также другие методы одномерной минимизации, которые можно найти, например, в [1, 7].

Градиентные методы

Пусть функция  непрерывно дифференцируема на ,
т.е. .

Процесс градиентного (наискорейшего) спуска замедляется по мере приближения к . Задача одномерной минимизации в методе наискорейшего спуска может быть решена методом золотого сечения. Сходимость методов утверждается следующей теоремой.

Теорема 1 [2]. Если в задаче (11.1) , функция  ограничена снизу, а ее градиент удовлетворяет условию Липшица , тогда при любом начальном приближении  последовательность , полученная методом градиентного (наискорейшего) спуска, обладает следующим свойством .

Из теоремы следует, что градиентные методы находят стационарную точку целевой функции и требуется в этой точке проверить выполнение достаточных условий минимума функции. Сходимость к точке минимума можно гарантировать только для сильно выпуклых функций. Недостатком методов является уменьшение скорости сходимости по мере приближения к . Скорость сходимости для сильно выпуклых функций оценивается
как 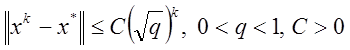 – константы.

Метод покоординатного спуска и метод Гаусса-Зейделя

По-видимому, наиболее простым из детерминированных способов выбора направления спуска является выбор в качестве  одного из координатных векторов , , вследствие чего у вектора  на каждой итерации изменяется лишь одна из компонент, так как у вектора  только j-я компонента равна единице, а остальные нулю. Геометрически спуск осуществляется по ломаной, состоящей из отрезков прямых, параллельных осям координат.

Сразу отметим, что в качестве  выбирается то из двух направлений , , которому соответствует неравенство

Алгоритм покоординатного спуска

0. Задать начальное значение , выбрать критерий остановки и задать точность .

1. Осуществляем n итераций по каждой из координат

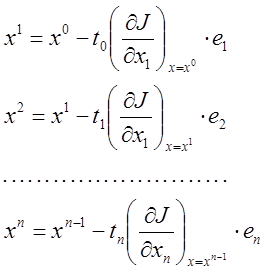
2. Если требуемая точность достигнута, тогда вычисления заканчиваем и , если нет, то переходим к шагу 1.

Выбор шагов  осуществляется или из условия (11.8) (метод покоординатного спуска), или из решения задачи одномерной минимизации
(метод Гаусса-Зейделя).

Теорема 2 [7]. Пусть функция  выпукла и непрерывно дифференцируема на , а начальное приближение  таково, что множество  ограничено. Тогда последовательность , полученная методом покоординатного спуска, минимизирует функцию  и сходится к множеству .

Методы покоординатного спуска особенно эффективны для сепарабельных функций:

.

Недостатки этого метода аналогичны недостаткам метода градиентного спуска.

Метод сопряженных градиентов

Определение. Направления  и  называются сопряженными относительно матрицы A, если .

Заметим, что A-сопряженное направление к заданному вектору
не единственно.

Для системы сопряженных векторов  выполнено

В методе сопряженных градиентов за направления спуска  выбирается сопряженное направление к некоторой матрице.

Сначала рассмотрим метод сопряженных градиентов для квадратичной функции . Здесь A – симметричная, положительно определенная матрица. В качестве направлений будем выбирать сопряженные направления к матрице квадратичной формы A.

Алгоритм

Пусть задано , положим , .

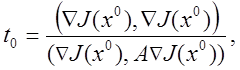
, где  .

, где   .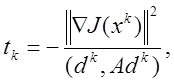

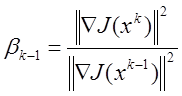Можно показать, что этот метод для квадратичной функции сходится за конечное число шагов к точке минимума.

Теперь рассмотрим алгоритм для не квадратичной функции .
Шаг  выбирается из условия . Для квадратичной функции этот минимум единственный и был найден аналитически, а для произвольной функции этого сделать нельзя, поэтому на каждом шаге алгоритма придется численно решать эту задачу одномерной минимизации.

Алгоритм Полака-Ривьера

0. Пусть задано , .

1. , где :  , ,   

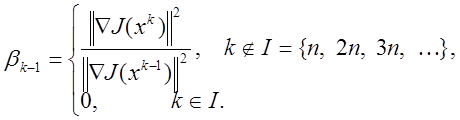
Теорема 3 [2, 7]. Если функция  ограничена снизу, а  удовлетворяет условию Липшица, то для любого начального приближения  последовательность , полученная методом Полака-Ривьера,  сходится к некоторой стационарной точке функции .

Следствие [2]. Пусть выполнены условия теоремы, тогда если
функция  является сильно выпуклой, то алгоритм Полака-Ривьера сходится к точке минимума .

Метод сопряженных градиентов сходится быстрее, чем метод наискорейшего градиентного спуска, но требует на каждой итерации большего числа вычислений.

Метод стохастической аппроксимации

На практике часто встречаются задачи, для которых неприменимы классические методы оптимизации. Особенности таких задач связаны
с отсутствием полной информации о целевой функции, о ее производных
и с негладким характером этой функции. Кроме того, даже для точно известных функций из-за различных погрешностей можно вычислять значения функции и ее производных лишь приближенно. Весьма усложняется решение задачи в тех случаях, когда на значение функции
в каждой точке накладываются случайные ошибки. Такая ситуация, например, имеет место в результате измерения какой-либо физической величины. В этих случаях для поиска минимума целесообразно использовать метод стохастической аппроксимации.

Опишем один из вариантов этого метода. Будем считать, что точные значения функции  могут быть измерены в любой фиксированной
точке  и равны некоторой случайной величине . Тогда для поиска минимума  на  может быть использован следующий итерационный метод:

(11.10)

где последовательности ,  заданы и удовлетворяют условиям

(11.11)

Например, здесь можно взять , .

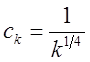Следует заметить, что в тех случаях, когда слева от точки минимума функция имеет крутой спуск, справа – крутой подъем, а на остальных участках  изменяется медленно, сходимость метода (11.10) ухудшается.
В самом деле, значительная часть времени будет затрачена на чрезмерно медленные спуски на пологих участках и последующие большие скачки через точку минимума с попаданием на другой пологий участок. В таких ситуациях следует модифицировать метод следующим образом: