Математика. Часть 4 (Вычислительная математика): План-конспект лекционного курса, страница 13

(8.6)

где . Чем больше величина , тем с большей вероятностью оценка интеграла будет удовлетворять приведенному неравенству.

Полученное соотношение дает способ вычисления интеграла как среднего арифметического случайных величин , т.е.

(8.7)

Кроме того, из соотношения (8.6) следует, что оценка погрешности вычисления интеграла носит вероятностный характер. Значение коэффициента  в соотношении (8.6) зависит от величины доверительной вероятности  и приведено в таблице для нескольких значений этого коэффициента.

Значение  выбирается заранее, до вычисления погрешности вычислений по методу статистических испытаний. Вероятностная оценка 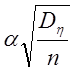 погрешности метода зависит от дисперсии случайной величины ,
не зависит от кратности интеграла и убывает пропорционально .

Неизвестная величина  в выражении (8.6) может быть оценена
в процессе вычислений по соотношению (8.5), если заменить входящие
в него математические ожидания на их оценки типа (8.7). Тогда

(8.8)

Возможность сравнительно простой оценки погрешности в процессе вычислений является важным достоинством метода статистических испытаний. Другим достоинством метода является то, что оценка погрешности не зависит от кратности интеграла. Это делает метод статистических испытаний более предпочтительным, чем метод Симпсона уже для пяти кратных интегралов.

Для сопоставления метода статистических испытаний с интерполяционными формулами вычисления интегралов можно воспользоваться следующей оценкой. При вычислении интеграла кратности S методом Монте-Карло требуется  операций, где m – число операций, необходимых для вычисления одного значения подынтегральной функции по одному измерению, n – число испытаний. С использованием интерполяционных формул требуется  операций, где k – число узловых точек по одному измерению.

Следует, однако, иметь в виду одно обстоятельство. При вычислении интеграла методом статистических испытаний практическое значение имеет относительная погрешность результата

,

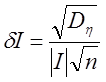зависящая от величины дисперсии. С увеличением кратности интеграла величина отношения  может существенно возрастать. Так, для интеграла

справедливо соотношение

Подробнее см.: 4–6.

Тема 9. Численное решение обыкновенных
дифференциальных уравнений

Основные вопросы темы

1. Постановка задачи.

2. Метод конечных разностей. Порядок точности разностной схемы.

3. Метод Эйлера.

4. Метод Рунге-Кутты.

5. Многошаговый метод Адамса.

Рассмотрим задачу Коши:

(9.1)

Здесь первое уравнение – это обыкновенное дифференциальное уравнение n-го порядка, если его можно записать в виде ,
то уравнение будет разрешенным относительно старшей производной.

Актуальность задачи Коши для многих областей явилась причиной разработки для ее решения большого количества методов. Рассматриваются две группы численных методов решения задачи Коши:

·  одношаговые методы, в которых для нахождения решения в некоторой точке отрезка используется информация лишь в одной предыдущей точке. К этим методам относятся методы Эйлера и Рунге-Кутты;

·  многошаговые методы, в которых для нахождения решения
в некоторой точке отрезка используется информация о решении
в нескольких предыдущих точках. К таким методам относится
метод Адамса.

Рассмотрим применение этих методов для решения одного дифференциального уравнения. Алгоритм для случая систем дифференциальных уравнений легко получается из алгоритма решения одного уравнения.

Необходимо отметить, что численные методы напрямую можно применять только к хорошо обусловленным задачам, т.е. таким задачам,
решение которых мало изменяется в случае малого изменения начальных условий. В противном случае небольшие ошибки, которые неизбежны
при решении задачи, могут существенно изменить решение.

В качестве плохо обусловленной задачи рассмотрим решение следующей задачи Коши на отрезке [0, 100]:

Общим решением этого уравнения является

Из начального условия находим, что , поэтому . Предположим, что начальное условие изменилось . Следовательно, изменится и постоянная c в общем решении. В этом случае  
и , т.е изменение начального условия на  изменило
решение в конечной точке на 35 порядков.

Метод конечных разностей.

Порядок точности разностной схемы

Численное решение обыкновенных дифференциальных уравнений
во многих случаях осуществляется методом конечных разностей. Метод конечных разностей сводит решение дифференциальных уравнений
к решению линейных или нелинейных уравнений с достаточно разреженными матрицами (матрицы, содержащие большое количество нулей). При этом построение решения осуществляется в три этапа.

·  Область непрерывного изменения аргумента (или аргументов)
заменяется дискретным множеством точек, называемых разностной сеткой. В разностной сетке выделяются внутренние и граничные узлы. Решение ищется во внутренних узлах, а в граничных
узлах значение искомой функции задается при аппроксимации граничных условий исходной дифференциальной задачи. Функция дискретного аргумента, определенная на разностной сетке, называется сеточной функцией.

·  Дифференциальные уравнения и граничные условия заменяются по определенным правилам своими разностными аналогами. Разностные операторы, соответствующие дифференциальному уравнению, записываются во внутренних узлах сетки. Разностные операторы, соответствующие граничным условиям, записываются
в граничных узлах. В результате получается система алгебраических уравнений, число которых пропорционально числу внутренних узлов разностной сетки.

·  Осуществляется решение системы алгебраических уравнений
каким-либо из известных методов. В большинстве случаев полученная система уравнений является системой линейных алгебраических уравнений очень большого порядка (как правило, ), но с весьма разреженной матрицей.

В случае нелинейных систем итерационные процедуры, как правило, сводят их к линейным системам.