Решение уравнения с одним неизвестным, страница 7

7. Сформируйте заголовок ИТИ путем вставки текстового блока и копии блока с решаемым уравнением типа (5.2). Вычислением длины какого-либо столбца (на рис. 5.2 – первого) убедитесь, что ИТВ является расчетной таблицей, позволяющей обращаться к любой ее ячейке.

Вставьте также название таблицы путем копирования уравнения и вставки текстового блока.

Примечания к разд. 5.1.2. 

1. Программный комплекс рис. 5.2 (элементы 1…7) может обеспечить вычисление зависимости корней полиномиального уравнения любой степени (от 2 до 99) от параметра «а» с практически любым количеством его значений и при вхождении «а» в любой коэффициент (коэффициенты) полинома уравнения в виде любой вычислимой Mathcad функции (см. уравнение (5.2) и рис. 5.2) .

2. Для получения объявленного в п.1 решения необходимо:

·  в п. 1 комплекса записать полином , векторы vn и «а» в соответствии с задаваемым уравнением;

·  в п. 2 комплекса также следует привести вектор v1 в соответствие с задаваемым уравнением.

 

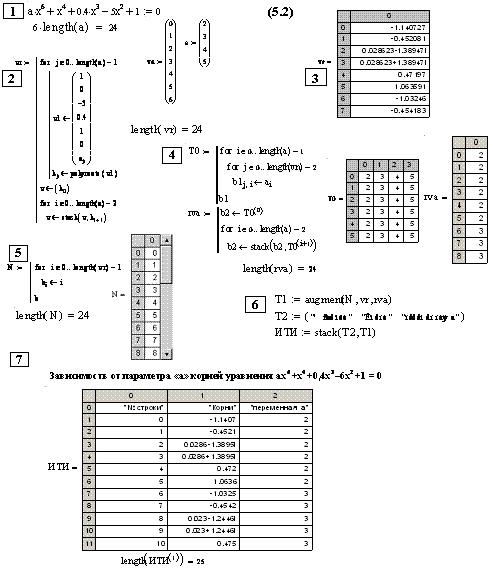Рис. 5.2. Этапы вычисления зависимости корней полиномиального уравнения (5.2)                                 от параметра «а»

5.1.3. Исследование функциональной зависимости                                          корней уравнения от нескольких параметров

Возможны два вида зависимости: при переборе всех сочетаний значений параметров и при сочетании только равноместных значений, когда оба параметра представлены векторами одинаковой длины. Второй случай назовем квазивекторизационным вычислением корней (см. ключевые термины разд. 5).

Зависимость при всех сочетаниях значений двух параметров

(параметры: а = 2; 3; 4 и 5; б = –5 и 10,3)

Программа исследования состоит из двух блоков:

·  вычисление зависимости корней от параметров «а» и «б» с выдачей Расчетной таблицы (вектор корней)  q3 – рис. 5.3 (справа –  фрагменты начала и конца таблицы; общее количество корней 48);