![]() Этапы 2 и 3 на
5.14 при вводе программы следует объединить: они введены для повышения компактности
комплекса при расположении рисунков в Пособии. Знаками
Этапы 2 и 3 на
5.14 при вводе программы следует объединить: они введены для повышения компактности
комплекса при расположении рисунков в Пособии. Знаками ![]() и в программе krd2рр(n) отмечены
дополнительные и измененные строки по сравнению с программой krd2р(n).
и в программе krd2рр(n) отмечены
дополнительные и измененные строки по сравнению с программой krd2р(n).
Отдельные вычисления
производной невязки и абсолютной погрешности корней не выполнялись, однако, при
необходимости их можно вставить в виде строк, формирующих расчетные и промежуточные
векторы соответственно vpr, vdr и ppr, pdr из программы этапа 2 рис. 5.6
(но без векторизации выражений) и их компоненты в места программы krd2рр(n), отмеченные
знаком ![]() .
.
Как следует из расчетных таблиц комплексов krd2р(n) и krd2рр(n) (этапы 4 рис. 5.13 и 5.15), для 4 сочетаний параметров уравнение типа (5.14) не имеет корней.
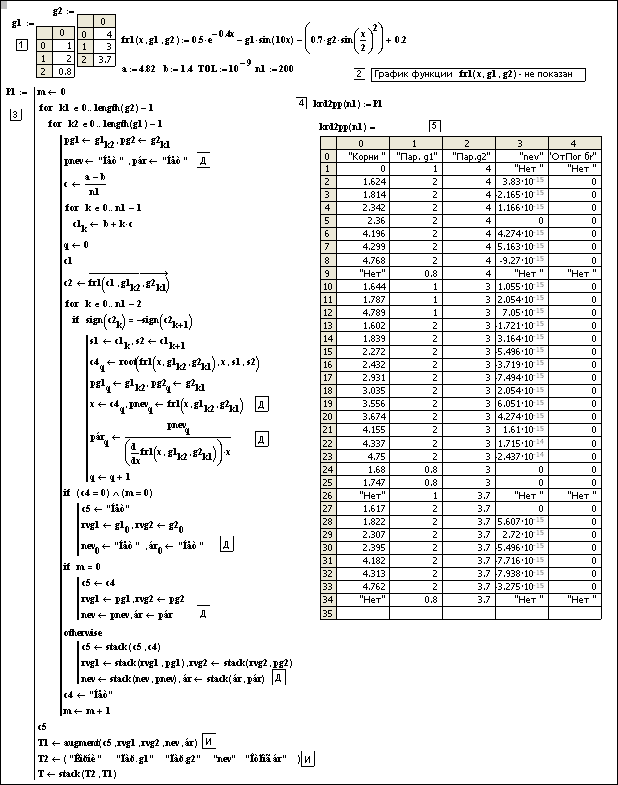
Рис. 5.14.
Комплекс krd2pр(n) исследования зависимости корней трансцендентного уравнения
типа (5.14) от 2 параметров g1, g2 с выдачей сочетаний параметров и относительной погрешности
для каждого корня. Этап 4 введен для сокращения места под программой. Знаками ![]() и
и ![]() в программе krd2рр(n) отмечены
дополнительные и измененные строки по сравнению с программой krd2р(n) рис. 5.12
в программе krd2рр(n) отмечены
дополнительные и измененные строки по сравнению с программой krd2р(n) рис. 5.12
(для работы программы Р в Mathcad 2001 следует в строках с двумя операторами (3, 12, 14 и т.д.) заменить запятую на пробел или каждый оператор разместить на отдельной строке)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.