Решение уравнения с одним неизвестным, страница 25

Уравнение с одним параметром

На рис. 5.15 (этапы ввода–вывода пронумерованы) представлен программный комплекс исследования krd1pp(n) с выдачей значений параметра, невязки nev и относительной погрешности вычисления корней бr для уравнения с одним параметром g1:

                 fr1(x1,g1) = g1×e^–0,4х1×cos(4x1) – 1,1×sin(8x1) – 0,7×2×sin((x1/2)²) = 0.                                 (5.15)

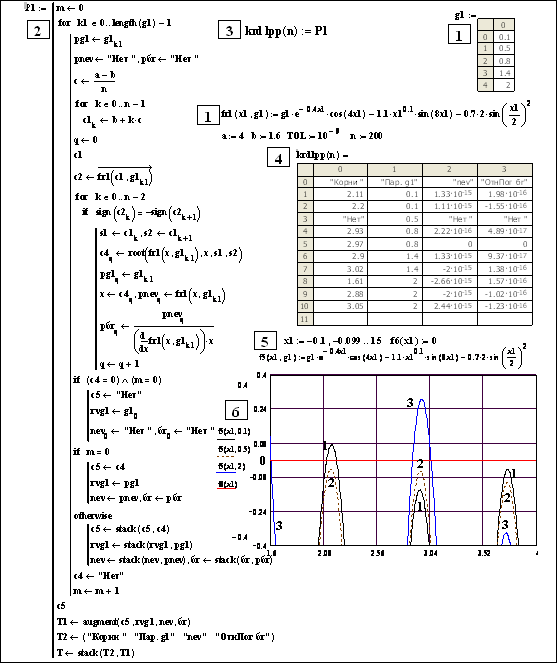
Рис. 5.15.  Комплекс krd1pp(n) вычисления зависимости корней трансцендентного уравнения типа (5.15) от параметра g1 c выдачей таблицы корней, значений параметра, невязки и относительных погрешностей корней

(для работы программы Р1 в Mathcad 2001 следует в строках с двумя операторами (4, 13, 16 и т.д)  заменить запятую на пробел или каждый оператор разместить на отдельной строке)

Уравнение с тремя параметрами

На рис. 5.17 и 5.18 (этапы ввода–вывода пронумерованы) представлен программный комплекс исследования krd3pp(n) с выдачей значений параметров, невязки nev и относительной погрешности вычисления корней бr для уравнения с 3 параметрами g1, g2, g3:

                                fr3(x1,g1,g2,g3) = g1 + g2×tan(sin(7x)) - 2×g3×cos(0,2x) = 0.                                   (5.16)

Этапы 2 и 3 можно соединить вместе, удалив промежуточную переменную Р1.

Правила применения комплекса krd3pp(n) аналогичны правилам применения комплекса krd2(n) из разд. 5.2.4.

 

Рис. 5.16.  Комплекс krd3pp(n) вычисления зависимости корней трансцендентного уравнения типа (5.16) от параметров g1, g2, g3 c выдачей таблицы корней, значений параметров, невязки и относительных погрешностей корней (первая часть комплекса, вторая – на рис. 5.17). Стрелки – разрыв в программе (сделан средствами пакета Word)

(для работы программы Р1 в Mathcad 2001 следует в строках с двумя и более операторами (4, 6, 15 и т.д.)  заменить запятую на пробел или каждый оператор разместить на отдельной строке)