Автоматическое вычисление зависимости корней от двух параметров того же уравнения (5.14) в диапазоне неизвестной х от 1,4 до 4,82 комплексом krd2(n) представлено на рис. 5.12 (этапы пронумерованы). Этап 5 – проверочное вычисление корней для каждого сочетания значений параметров по отдельности обычным комплексом krd(n), копированием из расчетной таблицы и вставкой данных в РДМ (вставляются в виде матрицы). Из сравнения данных таблиц этапа 4 с данными матриц этапа 5 видно, что комплекс вычислил все корни из заданного промежутка для всех сочетаний значений параметров g2, g3.
Основу комплекса krd2(n) составляет программа этапа 2, представляющая собой соединение двух циклов for с модифицированной программой комплекса krd(n) в виде 2-й программной линейки. В циклах формируется сочетание значений двух переменных параметров, а в программе линейки: вычисляется
вектор корней функции, соответствующей заданному сочетанию, вектор корней текущего сочетания встраивается в результирующий вектор корней расчета, далее производится замена вектора корней текущего сочетания на скаляр при переходе к новому сочетанию, выполняются несколько редакторских операций при формировании общего вектора корней.
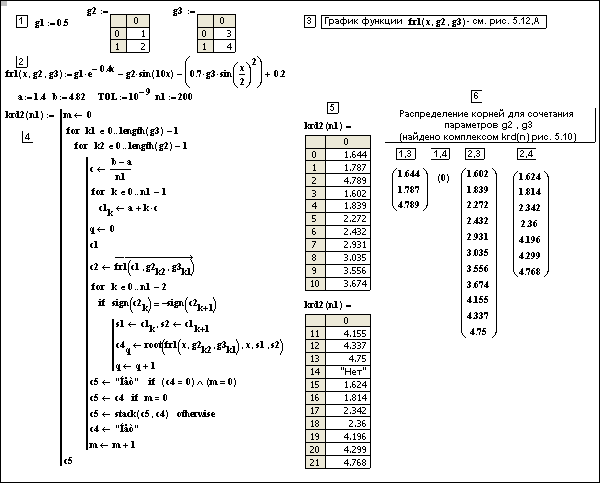
Рис. 5.12. Программное вычисление зависимости корней уравнения (5.14) от 2 параметров g2,g3 в диапазоне неизвестной х от 1,4 до 4,82 комплексом krd2(n). Этап 3 – построение графика для контроля количества вычисляемых корней, 5 – расчетная таблица всех корней уравнения (5.14), этап 6 – корни, вычисленные krd(n) для сочетаний значений параметров по отдельности
(для работы программы krd2(n1) в Mathcad 2001 следует в 11–й строке с двумя операторами заменить запятую на пробел или каждый оператор разместить на отдельной строке)
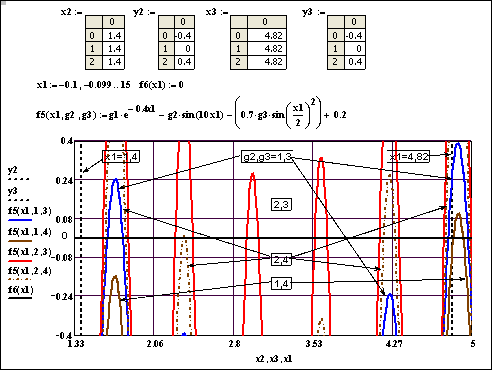
Рис. 5.12, А. График функции fr1(x,g2,g3) из рис. 5.12. Граничные линии х1=1,4 и х1=4,82 построены посредством 4 векторов соответственно х2, у2 и х3, у3
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.