Для этой цели можно применить оба решателя уравнений из пакета или упомянутый выше комплекс krd(n). Решатели, как известно, дают только один корень (они – локальные решатели): следовательно, каждому сочетанию параметров может быть сопоставлен только один корень, т.е. корней может быть обнаружено столько, сколько сочетаний значений параметров. Если у уравнения несколько корней, т.е. все они, за исключением одного, в процессе текущего решения принципиально не вычисляются. Для их поиска нужно менять начальные условия: менять границы участка расположения нового корня для диапазонного root или брать другое приближенное значение корня для локального root – это все ручные операции.
Комплекс krd(n) позволяет вычислять все корни автоматически, однако в силу существующих ограничений в Mathcad, комплекс должен быть модифицирован под задачу исследования.
g1×e-0,4×x – g2×sin(10×x) – 0,7×g3×sin(x/2)2 +0,2 = 0. (5.14)
На рис. 5.11 показано исследование уравнения (5.14) локальным root: определение зависимости корней от 2 параметров g2,g3 (этапы ввода групп вычобъектов пронумерованы). Этапы 1 и 2 – собственно исследование, 3 и 4 – контроль выданных корней посредством графика. Номера функций на графике соответствуют порядку их расположения на оси ординат сверху вниз. Функция № 6 введена для выделения нулевой линии, которая при заданных пределах автоматически не вычерчивается пакетом.
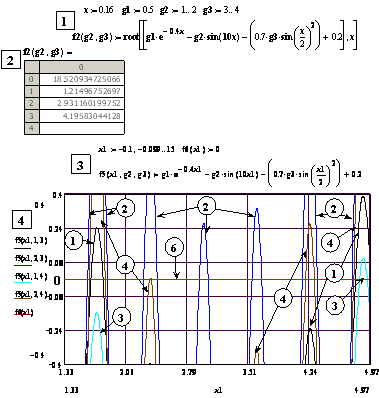
Рис. 5.11. Исследование зависимости корней трансцендентного уравнения (5.14) от 2 параметров g2, g3 посредством локальной функций root. Номера функций соответствуют порядку их расположения на оси ординат сверху вниз
Как следует из рисунка, число сочетаний значений параметров – 4, столько же корней выдает и решатель, в то время как число корней в диапазоне неизвестной х от 1,4 до 4,82 равно 21. Сочетания значений параметров g2, g3: 1–3, 1– 4, 2–3, 2– 4. Начальное приближение корня – 0,16. Найденное значение для первого сочетания – 18,5 (таблица этапа 2), оно не соответствует начальному приближению (см. кривые 1 функции уравнения для 1-го сочетания параметров): на участке х от 1,33 до 4, 97 находятся 7 корней, расположенных ближе к 0,16 по сравнению с 18,5. При остальных сочетаниях параметров найденные корни ближе к начальному приближению, чем первый, но при этом существуют и другие, расположенные ближе, чем найденный. Например, для второго сочетания значений 1– 4 между найденным корнем 2,93 и началом отсчета графика расположены еще 4 корня (см. кривые 2 рис. 5.11 для этого сочетания значений параметров).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.