Решение уравнения с одним неизвестным, страница 23

4.  Задайте некоторое число участков разбиения n1 диапазона поиска корней a,b,  контролируя необходимую длину участка t_n  из неравенства (5.13) по графику функции уравнения для заданного сочетания параметров.

 

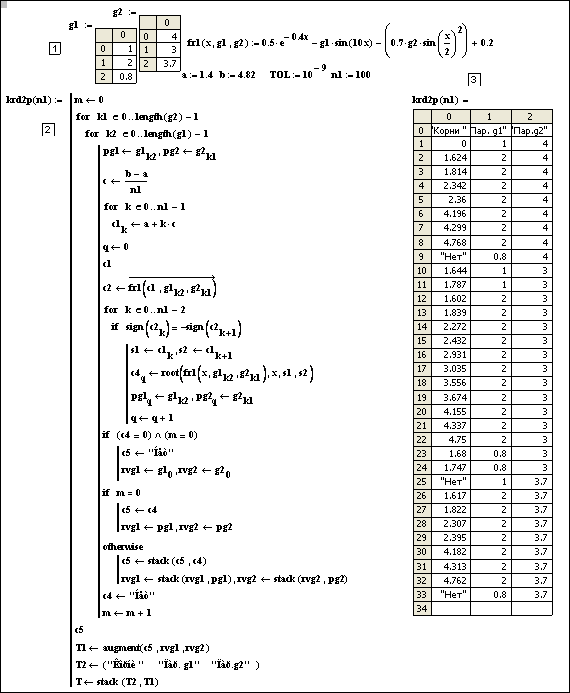Рис. 5.13. Комплекс krd2p(n) исследования зависимости корней трансцендентного уравнения типа (5.14) от 2 параметров g1, g2 с выдачей сочетаний параметров для каждого корня. Переменная “Нет” – отсутствие корней для данного сочетания параметров

(для работы программы Р в Mathcad 2001 следует в строках с двумя операторами (4, 13, 15 и т.д.)  заменить запятую на пробел или каждый оператор разместить на отдельной строке)

5.  Нажатием клавиши <F9> запустите вычисления при этом, вызов расчетной таблицы комплекса krd2(n) = должен находиться в видимой части окна пакета.

6.  Зафиксируйте количество корней, выданных комплексом и увеличив число участков в 5…10 раз,  повторите вычисления. Если число корней в расчетной таблице осталось прежним, то вычисления можно считать успешно законченными.

5.2.5. Исследование зависимости корней уравнения                                                                  от двух параметров комплексами krd2р(n) и krd2рр(n)                                                                                     с отображением погрешностей и сочетаний параметров

Для уравнения типа (5.14) при большом числе значений параметров g1и g2 (десятки и более) отслеживать в расчетной таблице границы сочетаний практически невозможно даже при наличии графика. В комплексах krd2р(n) и krd2рр(n) необходимость отслеживания исключена. Первый комплекс (рис. 5.13) выдает наряду с корнями сочетания значений параметров, а второй (рис. 5.14, 5.15) – сочетания невязки и относительной погрешности вычисления корней.