Для оценки границ поддиапазона каждого корня или его приближенной величины используется измерительная панелька Trace. В случае неразличимо близкого расположения корней на отдельных участках следует увеличивать их посредством панельки масштабирования Zoom. Если выделяются границы поддиапазона корня, то для вычисления его величины применяется диапазонный решатель root(f(х,p1,p2,…,pN),х,a,b), если же определяется его приближенная величина – то решатель локальный root(f(х,p1,p2,…,pN),хН), куда вместо хН вставляется приближенное значение корня, скопированное в буфер панелькой Trace. Последний метод предпочтительнее первого из–за сокращения в 2 раза буферных операций.
3. Применитьпрограммный комплекс krd(n) (корни в диапазоне), выполняющий перечисленные в п. 1 действия для вещественных корней в автоматическом режиме и включающий Начальный блок и Собственно программу krd(n) (рис. 5.10). При большом количестве корней применение комплекса становится единственно правильным. В результате комплекс создает вектор корней уравнения (5.8) в заданном диапазоне неизвестной, который затем можно использовать для автоматического вычисления погрешности корней по программе этапов 2, см. рис. 5.6 или 5.8.
Комплекс можно также применять для программного исследования зависимости вещественных корней уравнения (5.8) от параметров.
Начальный блок состоит из записей (рис. 5.10): функции уравнения fr(x) (левой части уравнения (5.12) – первая строка), правой и левой точек диапазона и локального значения переменной TOL, определяющей точность вычисления корней именно в заданном комплексе.
fr(x) =2×sin(10×x) = 0 (5.12)
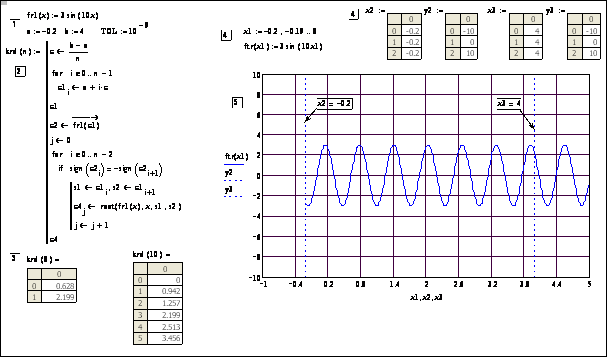
Рис. 5.10. Комплекс krd(n) отделения и вычисления вещественных корней
уравнения fr(x) = 0 (на примере уравнения (5.12)) для х Î [b, a] при ручном вводе числа участков разбиения n и величины системной переменной TOL
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.