Оба решателя находят только один корень. Для вычисления других корней следует изменять начальное приближение вручную или использовать программные методы (см. ниже), см. также «Принципы решения уравнений…» в начале разд. 5.
Примечание. Если уравнение (5.8) имеет несколько корней, то поиск непересекающихся областей, содержащих эти корни, (отделение корней) осуществляется в полуавтоматическом или программном режимах с последующим вычислением корней посредством диапазонной root в ручном или программном вариантах.
Следует различать:
решение уравнения (вычисление его корней);
исследование уравнения (вычисление зависимости корней от параметров).
f(x) = tg(x) – 3sin(10x) - 2 sin2 (x/2) = 0. (5.11)
На рис. 5.9 показано вычисление отдельных корней уравнения (5.11) посредством соответственно диапазонной и локальной функций root (этапы вычисления пронумерованы). Этапы 1 и 2 выполняются раньше других. Переменная х1 графика носит имя, отличное от искомой переменной х решателей для исключения ее влияния на решатели. На графике корни, вычисляемые в поз. 3…5, 7, 10, помечены номерами этих позиций.
В диапазоне х (3…4) заключены 3 корня уравнения (5.11), но диапазонный root (поз. 3) находит только один, ближайший к левому пределу диапазона 3. В п. 4 и 5 – определение двух различных корней этого уравнения подбором величины начального приближения хН корня (1 и 2,5) для локального решателя root.
Поз. 6…10 демонстрируют взаимодействие начального приближения и локального минимума функции уравнения на вычисление разных корней уравнения. Рядом с начальным приближением указано значение функции уравнения ftr(x); локальный минимум при х = 0,78.
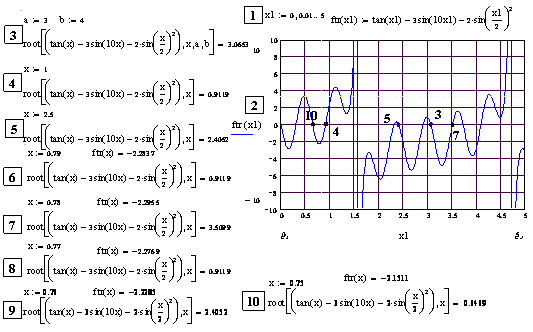
Рис. 5.9. Вычисление корней трансцендентного уравнения (5.11) посредством двух типов решателей root с использованием графика для определения начальных приближений корней
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.