Решение систем алгебраических и трансцендентных уравнений, страница 30

Пример использования показан на рис. 6.10 и 6.11 для Mathcad 13 и 2001 соответственно. Карта используется для определения количества корней в заданной области, которые нужно вычислить, для оценки оставшихся невычисленными корней после ряда сеансов решения, для индивидуального вычисления отдельных корней, не вычисляемых в сеансах сканирования по неизвестным, для выявления корней, не вычисляемых данным решателем Mathcad. К таким корням, например, относятся корни №№ 2, 4, 8, 25 и 28 на рис. 6.10: несмотря на близкое к корню начальное приближение, выдается другой корень, иногда весьма далеко отстоящий от начального приближения (см. табл. 6.2).

 

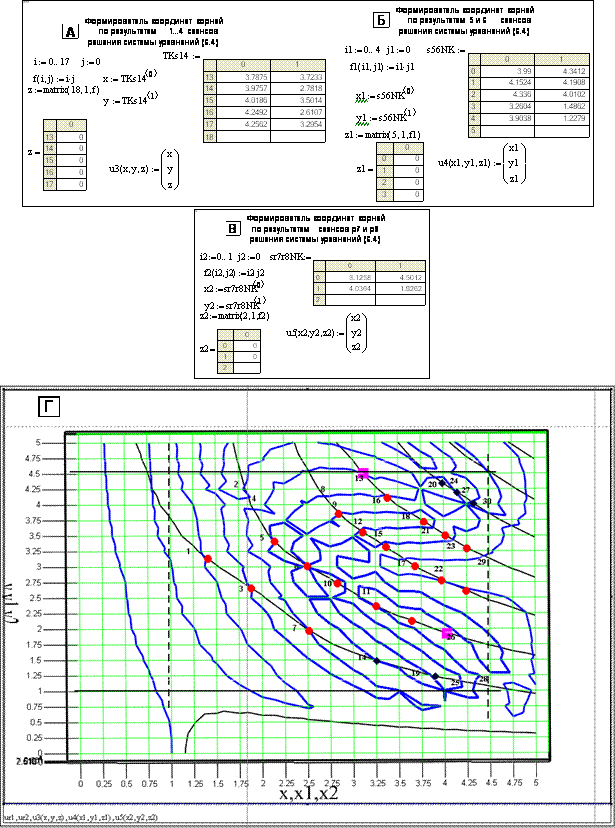Рис. 6.10. Отображение на контурной карте результатов вычисления корней                                                            системы уравнений (6.4)  в Mathcad 13. Корни сеансов:       – 1…4;       – 5, 6;       – р7, р8

Указанные задачи решаются на основе построения групп найденных корней в области поиска и придания видимого отличия каждой группе корней.

Этапы построения группы корней на контурной карте

1.  Ввод формирователя группы корней в РДМ (рис. 6.10, А…В). Таблицы с координатами корней – это входные таблицы. Их содержание получается копированием соответствующих ячеек Word-таблицы ПРСУ (например, столбцов 4 и 5 сеансов 1…4) в буфер и последующей вставкой командой Paste Table Контекстного меню. Рядные переменные i и j, функции f(i,j) и matrix нужны для создания нулевого вектора z с числом нулевых компонент, равным числу отображаемых корней.

2.  Ввод функции отображения выбранных корней (например, u3(x, y, z)) в контурную карту. Функция вставляется в строку вставки внизу контурной карты в место ввода, появляющееся после того, как справа от ur2 будет поставлена запятая. После ввода функции Mathcad изменит 2-мерный график на 3-мерный (линии контуров при этом исчезнут из-за ненастроенности шкалы оси z.), которому следует придать вид, аналогичный рис. 6.10, Г.