Решение систем алгебраических и трансцендентных уравнений, страница 3

Для комплексных переменных предельное число неизвестных в системе уравнений сокращается в 2 раза по сравнению с вышеуказанным.

Предельные возможности решателя lsolve(…) по числу неизвестных были исследованы на примере системы линейных уравнений с 450 неизвестными. Результат – на рис. 6.1 (этапы решения пронумерованы).

1.  Ввод в РДМ вектора-столбца m 450 случайных чисел, распределенных по нормальному закону со средним значением 1 и среднеквадратическим отклонением 2.

2.  Формирование таблицы Z гнездовых матриц с увеличивающимся на 1 для каждой следующей строки количеством столбцов; последняя матрица Z₄₄₉ таблицы – квадратная с числом элементов 450х450, которые распределены по нормальному (гауссовскому) закону.

                                                                            

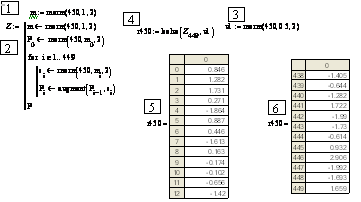
Рис. 6.1. Решение системы 450 линейных уравнений решателем lsolve(Z₄₄₉,v1)

3.  Формирование вектора v1 правых частей (свободных членов) системы линейных уравнений: у вектора 450 компонент, значения которых распределены по нормальному закону с параметрами из п. 1.

4.  Ввод решающей функции lsolve(Z₄₄₉,v1) решения системы 450 линейных уравнений, коэффициенты которых составляют квадратную матрицу Z₄₄₉, а правые части – вектор v1.

5.  Вызов решения: Mathcad выдает таблицу 450 корней (показаны первые 13). Время решения ~ 1…2 с (для компьютера Пентиум 4, частота 3 ГГц, ОЗУ 1 Гб).

6.  Копия таблицы из п. 5 – показаны последние 12 корней.

Как следует из рис. 6.1 решатель lsolve(…) обеспечивает решение системы линейных уравнений со значительно большим числом неизвестных, чем это следовало из справочника Mathcad [43]: 450 вместо 400. Судя по вычислениям, количество неизвестных в системе можно еще увеличивать, однако в этом процессе возникает проблема с расходованием ОЗУ компьютера – см. Свойства решателя… в разд. 6.1.

6.1. Системы линейных уравнений

Если система линейных уравнений имеет решение, то это решение всегда полное, так как является единственным.