Физические основы защиты информации от технической разведки, страница 64

1) несмотря на отсутствие сигнала, шум превосходит порог и принимается неправильное решение о наличии сигнала (ошибка первого рода),

2) хотя сигнал присутствует, но пороговый уровень не превышен и принимается ошибочное решение об отсутствии  сигнала (ошибка второго рода).

Обозначим вероятность ошибки первого рода через Р_о=Р(1|0) и вероятность ошибки второго рода через Р₁=Р(1|0). Для этих вероятностей можем написать формулы:

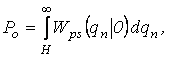
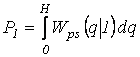  .           (3.36)

Средняя вероятность общей (суммарной) ошибки равна

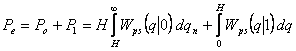,      (3.37)

а вероятность правильного обнаружения сигнала равна:

.                                (3.38)

Согласно критерию идеального наблюдателя пороговый уровень Н устанавливается таким, чтобы вероятность общей ошибки Р_е была минимальной и, соответственно, вероятность правильного решения максимальной. Таким образом, оптимальный характер идеального наблюдателя состоит в том, что он минимизирует вероятность суммарной ошибки или, иначе, максимизирует общую вероятность правильного решения.

Чтобы правая часть равенства (3.37) имела минимум, нужно приравнять производную по H нулю. В результате получим, что если для принятой реализации окажется

W_ps(H|1)/ W_ps(H|0)>1,                            (3.39)

то следует констатировать факт наличия сигнала, и наоборот.

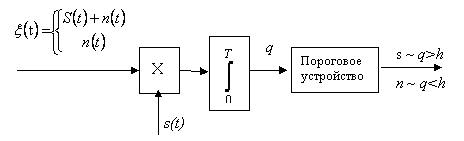
Рис. 3.3. Оптимальная схема для обнаружения детерминированного сигнала на фоне шума

Подставив в (3.39) выражения апостериорных вероятностей из (3.33) и (3.34), получим, что решение о наличии сигнала принимается при выполнении неравенства

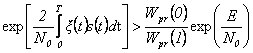.           (3.40)

Учитывая монотонный характер логарифмической функции и логарифмируя обе части этого неравенства, содержащего положительные величины, получим