При непрерывной обработке принятой реализации апостериорная вероятность наличия детерминированного сигнала (l =1) определяется формулой
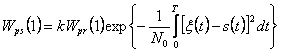. (3.33)
Апостериорная вероятность отсутствия сигнала (l=0), очевидно, равна
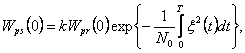(3.34)
причем
(3.35)
Хотя апостериорные вероятности содержат максимум сведений относительно наличия или отсутствия сигнала, однако практически от приемника-обнаружителя требуется просто один из двух ответов: есть сигнал или нет. Естественно считать, что решение о наличии или отсутствии сигнала должно приниматься путем сравнения апостериорных вероятностей по определенному правилу.
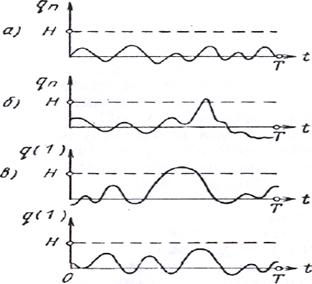
Для выяснения этого правила обратимся к рис. 3.2. На рисунке приведены четыре реализации случайного колебания: первые две изображают шум на выходе согласованного фильтра qп, адве другие - сумму сигнала и шума q=q(l). Пусть установлен некоторый порог Н. Для конкретных реализаций, приведенных на рисунке, замечаем, что шум в первой реализации не превышает порога. Во второй реализации хотя сигнала и нет, однако выброс шума превышает порог. В третьей реализации сумма сигнала и шума превышает порог, а четвертая реализация, несмотря на наличие сигнала, не достигает порога.
|
г) |
Рис 3.2. Четыре возможных случая при обнаружении
сигнала на фоне шума
Из рассмотренных четырех случаев в двух случаях (первом и третьем) будет принято правильное решение, а в двух (втором и четвертом) - неправильное. Если взять другой порог Н, то описанная ситуация может измениться.
Из такого качественного рассмотрения приходим к выводу, что при конечном значении энергии сигнала и наличии случайного шума принятие решения о наличии или отсутствии сигнала всегда сопровождается ошибками двух видов:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.