Физические основы защиты информации от технической разведки, страница 62

        ,                           (3.27)

,                                  (3.28)

где множитель k_D, зависящий только от D, подбирается так, чтобы предел имел смысл.

Осуществляя предельный переход при соответствующем подбореk_D, получим

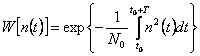,                    (3.29)

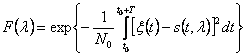.              (3.30)

Таким образом, при непрерывном наблюдении формула (3.12) принимает следующий окончательный вид:

                        (3.31)

где F(l) - функционал правдоподобия.

С учетом изложенного обоснуем оптимальную схему обнаружения сигнала для практически важного частного случая, когда сигнал носит детерминированный характер, а неизвестный параметр l  может принимать только одно из двух значений: l =1 (в принятом колебании присутствует сигнал) и  l=0 (в принятом колебании сигнал отсутствует).

Пусть принятое колебание x(t) представляет сумму

,                      (3.32)

где n(t) белый нормальный шум,  s(t) -  полезный сигнал известной формы (детерминированный сигнал), полностью расположенный на интервале наблюдения.

Что касается априорных сведений о параметре l, то будем полагать, что априорные вероятности  наличия и отсутствия сигнала W_pr(1) и W_pr(0)  известны.

По принятой конкретной реализации x(t) необходимо решить оптимальным (в некотором  смысле наилучшим) образом, какое именно значение имеет параметр l, т.е. присутствует  или отсутствует сигнал в принятой реализации. Иначе говоря, нужно найти такой метод обработки принятого колебания x(t), который бы позволял наилучшим образом обнаруживать наличие сигнала на фоне шума.