Физические основы защиты информации от технической разведки, страница 61

Вычислим сначала совместную плотность вероятности для случайных величин n_i, i=1, 2, …, m.Случайные величины n_i являются нормально распределенными и согласно (3.19) имеют следующие характеристики:

.

Поэтому совместная плотность вероятности имеет вид

.

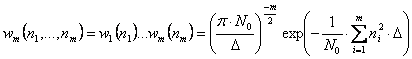(3.22)

Подставляя значения n_i из  (3.21) в (3.11) и учитывая, что якобиан преобразования от переменных n_i к переменным x_i    равен единице, получаем формулу для функции правдоподобия параметра l:

.     (3.23)

Таким образом, при дискретном наблюдении формула (3.12) принимает следующий окончательный вид:

,                       (3.24)

где

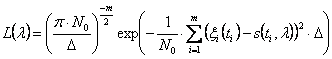.      (3.25)

Если параметр l может принимать несколько значений l₁, l₂, …, l_v, то в формулу (3.14) нужно подставлять функцию правдоподобия при соответствующем значении параметра l..

Путем аналогичных рассуждений нетрудно убедиться, что для сигнала (3.16), зависящих от нескольких параметров, функция правдоподобия, входящая в формулу (3.17), имеет вид:

.

(3.26) 

Рассмотрим теперь случай непрерывного наблюдения. Чтобы перейти к случаю непрерывного наблюдения, нужно в формулах (3.22), (3.25) и (3.26) перейти к пределу при D®0. При этом информация о случайном процессе x(t) будет заключаться в форме реализации, т.е. в том, какой конкретный вид имеет функция x(t) на интервале (t₀, t₀+T). Разумеется, что при непрерывном наблюдении в общем случае получаются более точные результаты, чем при дискретном, так как в случае непрерывного наблюдения используется информация, содержащаяся во всей реализации x(t), а не только в отдельных выборочных значениях x₁, …, x_m. При D®0 плотности вероятности W_m и w_m перейдут в соответствующие функционалы вероятности, а функция правдоподобия – в функционал правдоподобия. Введем для них следующие обозначения: