Из формул (3.12), (3.14) и (3.17) видно, что при известных априорных плотностях вероятностей нахождение апостериорной вероятности сводится к вычислению функции правдоподобия.
В том случае, когда принятое колебание представляет аддитивную смесь сигнала и шума, т.е.
![]() (3.19)
(3.19)
и многомерные плотности вероятности шума ![]() известны,
функции правдоподобия вычисляются сравнительно просто. В других же случаях их
вычисление представляет весьма сложную задачу.
известны,
функции правдоподобия вычисляются сравнительно просто. В других же случаях их
вычисление представляет весьма сложную задачу.
Далее мы ограничимся рассмотрением того важного, но частного случая, когда принятое колебание x(t) представляет собой аддитивную смесь полезного сигнала s(t) и нормального белого шума n(t). При этом значение спектральной плотности шума N0 будем предполагать известным.
Рассмотрим простейший метод дискретного наблюдения, когда отсчеты берутся через равноотстоящие отрезки времени. Разобьем интервал времени (t0, t0+T) равноотстоящими точками t1, …, tm, где ti -ti-1 = D = const, i=1,2, …, m. Обозначим средние за элементарный интервал времени значения колебания x(t), сигнала s(t, l ), и шума n(t) соответственно через
|
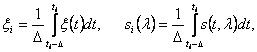
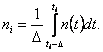 (3.20)
(3.20)
Очевидно, что
![]() (3.21)
(3.21)
Будем считать, что в выражении для функции правдоподобия (3.11) фигурируют указанные средние значения xi. При этом имеется ввиду, что в дальнейшем нас будет интересовать предельный случай D®0.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.