Физические основы защиты информации от технической разведки, страница 59

Отбрасывая левую часть равенства и учитывая, что  не зависит от интересующего нас параметра l, на основании формул (3.8) и (3.9) можно записать

,                  (3.10)

где коэффициент k определяется из условия нормировки.

Рассматриваемая, как функция от l, условная вероятность  называется функцией правдоподобия. При фиксированных значениях  она показывает, насколько одно возможное значение l более правдоподобно, чем другое. Обозначим функцию правдоподобия через L(l) :

 .                         (3.11)

Тогда формулу (3.9) можно записать в окончательном виде

,                       (3.12)

где

.                        (3.13)

Формула (3.12), по существу, представляет математическую запись теоремы Байеса, которая показывает, каким образом из априорных  данных и результатов анализа принятого колебания формируются  априорные знания.

Формула (3.12) может быть обобщена. Если параметр l может принимать только одно из нескольких дискретных значений l₁, l₂, …, l_v, то можно записать

          (3.14)

где

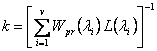.                          (3.15)

            Если сигнал зависит от m параметров l₁, l₂, …, l_m , т.е.

                           (3.16)

то формула примет вид:

             (3.17)

где

.         (3.18)