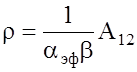Разработка методов многокритериального синтеза сигналов и устройств обработки, обеспечивающих робастные качественные показатели системы, страница 9

,                                                                                          (1.20)

где 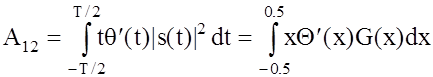,  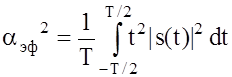‑ эффек­тив­ная длительность сигнала s(t), T ‑ длительность сигнала, 2b ‑ эффективная ширина спектра сигнала, q(t) ‑ закон изменения фазы сигнала, Q(x) ‑ фазовый спектр сигнала.

Величина r2 может изменяться от 0 до 1, причем максимальную скорость спада основного лепестка при доплеровском сдвиге имеют сигналы с r2 = 0. Отклик СФ у таких сигналов близок по форме к кнопочному.

Вообще проблема синтеза сигналов с r2 = 0 занимает важное место среди задач синтеза радиолокационных сигналов [8]. Это объясняется тем, что данные сигналы обеспечивают минимальные дисперсии измерения времени задержки  и доплеровского смещения частоты  при совместных измерениях времени запаздывания и доплеровского сдвига

,                           ,

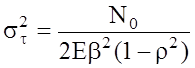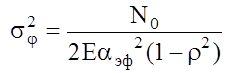где N0 ‑ СПМ шума, E ‑ энергия сигнала.

Обычно [8], синтез сигналов с нулевым коэффициентом частотно-временной связи осуществлялся исходя из условия

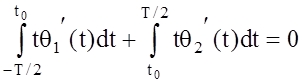,                                                               (1.21)

где,  и  ‑ производные от законов изменения фазы сигнала на интервалах [‑T/2; t0] и [t0; T/2] соответственно. При этом предполагается, что квадрат огибающей сигнала |s(t)|2 является четной функцией, что, как правило, выполняется для реальных сигналов.

Равенство (1.21) выполняется, в частности, при t0 = 0 и , т.е. сигналы с четным законом изменения частоты обладают нулевым коэффициентом частотно-временной связи. В то же время практическое использование подобных сигналов, например сигналов с V‑образным и параболическим законами частотной модуляции, затруднительно из-за высокого УБВ отклика СФ.

Существуют и другие, не обязательно четные, двунаправленные законы частотной модуляции, обеспечивающие нулевой коэффициент частотно-временной связи. Однако из-за жесткости условия r = 0 и однокритериального подхода к синтезу качественные характеристики получающихся сигналов получались неудовлетворительными [8].

В связи с этим решение задачи синтеза сигнала, робастного к модуляционным искажениям, предлагается искать в классе сигналов, минимизирующих функционал

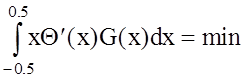                                                                          (1.22)

при заданных ограничениях. В этом случае, выбирая параметры сигнала, можно добиться компромисса между величиной коэффициента частотно-временной связи и другими качественные показателями сигнала.

В качестве последних логично использовать важные, с точки зрения радиолокационных приложений, параметры сигнала [8]: постоянную разрешения по времени TR и эффективную ширину спектра 2b

,                 .

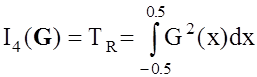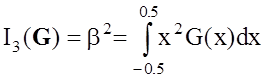Как уже отмечалось, указанные параметры определяют разрешающую способность и точность оценки времени запаздывания.

Из выражения (1.22) следует, что минимизация коэффициента частотно-временной связи достигается совместным выбором как СПМ сигнала, так и его фазового спектра. Однако для большинства применяемых на практике сигналов допустимо предположение о прямоугольности огибающей, т.е. |s(t)| = rect(t). В этом случае на основе метода стационарной фазы [8] можно получить

,

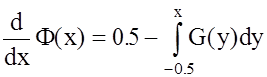т.е. свести задачу синтеза робастного сигнала к задаче синтеза СПМ. Если ввести обозначение

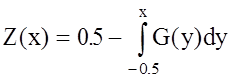,                                                                           (1.23)

то функционалы I3(G), I4(G) и I5(F, G) принимают вид

,                   ,

.

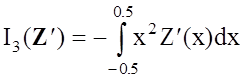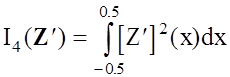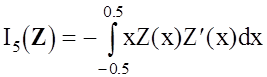В результате задача синтеза сигнала, робастного к модуляционным искажениям сводится к задаче векторной минимизации следующих функционалов

I(Z) = {I3(Z), I4(Z), I5(Z)}.

Аналогично рассмотренному выше, на основе метода рабочих характеристик [25] и в силу принципа взаимности изопериметрических задач определение рабочей поверхности сводится к нахождению экстремума функционала

I(G) = I4(G) + l17I3(G) + l18I5(G).                                                         (1.24)

Возможны два решения уравнения Эйлера-Лагранжа

,

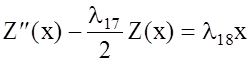которые являются необходимым условием наличия стационарной точки функционала (1.24):

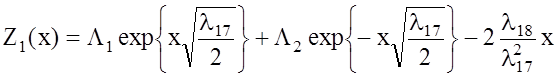, при l2 > 0 и (1.25)

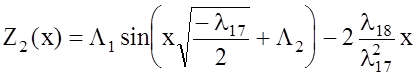, при l2 < 0,                   (1.26)

где L1 и L2 ‑ постоянные интегрирования. Наибольший интерес представляет решение Z2(x), т.к. оно включает в себя, как частные случаи, такие известные СПМ, как косинус с пьедесталом и rect(x).

Действительно, введем обозначения 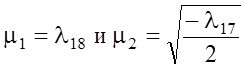, тогда искомая СПМ синтезированного сигнала

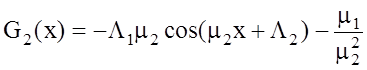.                                                    (1.27)

С учетом нормировки и условия (1.23) окончательно получаем

.                                   (1.28)

Используя данное выражение, легко найти остальные параметры сигнала:

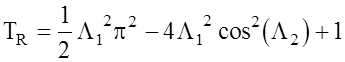,                                                        (1.29)

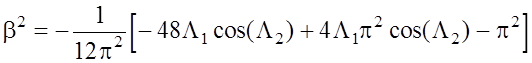,                         (1.30)

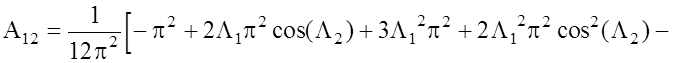
.                                          (1.31)

На рис. 1.15 приведено тело неопределенности синтезированного сигнала при r2 = 0.43 и отсутствии амплитудных модуляционных искажений. Из рисунка видно, что тело неопределенности имеет более высокую скорость спада, чем тело неопределенности рис. 1.13. На рис. 1.16 показано тело неопределенности синтезированного сигнала при введении амплитудных модуляционных искажений (an = 0.5 и ), аналогичных использованным при анализе сигнала с СПМ Хэмминга. Как следует из анализа рис. 1.14 и 1.16, введение амплитудных модуляционных искажений приводит к более существенному изменению тела неопределенности сигнала Хэмминга, чем синтезированного сигнала. Для иллюстрации этого на рис. 1.17 показаны зависимости ухудшения УБВ Dg отклика СФ от уровня амплитудных модуляционных искажений aMn, для сигнала с СПМ Хэмминга GH(x) ‑ кривая 1 и для синтезированного сигнала ‑ кривая 2. Из анализа рис. 1.17 следует, что синтезированный сигнал менее чувствителен к модуляционным искажениям, так при одинаковых уровнях амплитудных искажений УБВ сигнала GH(x) ухудшается на 5 ¸ 20 дБ, а синтезированного сигнала - только на 2 ¸ 10 дБ.