Разработка методов многокритериального синтеза сигналов и устройств обработки, обеспечивающих робастные качественные показатели системы, страница 19

Таким образом, задачу синтеза ФМн сигналов, обеспечивающих при обработке в СФ минимальную чувствительность к действию мешающих факторов можно рассматривать как задачу максимизации удельной энтропии сигнала при минимальном УБВ отклика фильтра. Т.е. при выполнении условия нормировки сигнала 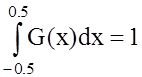 функционал (3.1) необходимо максимизировать.

Как указывалось выше, ФМн сигнал s(t) можно описать при помощи соответствующей ему дискретной последовательности . di = ± 1. СПМ ФМн сигнала также можно представить в виде вектора , тогда критерий (3.1) приобретает вид

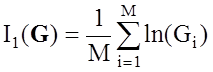.                                                                                (3.2)

Вводя эталонный отклик СФ в виде вектора , зададим корреляционный критерий приближения в виде

I6(D, R0) = ||ADD - R0||2,                                                                            (3.3)

где AD - матрица вида

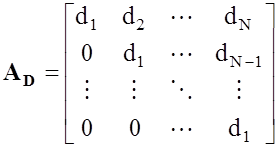,                                                                     (3.4)

а норма вычисляется в пространствах C, L2 или LP. Как показано в [6], наилучшей сходимостью к экстремуму обладают нормы в пространствах L2 и LP.

Исходя из вышесказанного, можно окончательно записать комбинированный критерий синтеза ФМн сигналов

I(D) = a1I6(D, R0) + (1 - a1)I1(G),                                                            (3.5)

где коэффициент a1 = 0...1 обеспечивает перераспределение веса отдельных критериев качества.

Экстремум функционала (3.5) искался методом покоординатного спуска. В результате были синтезированы последовательности D, максимизирующие удельную энтропию ФМн сигнала при заданном УБВ отклика СФ.

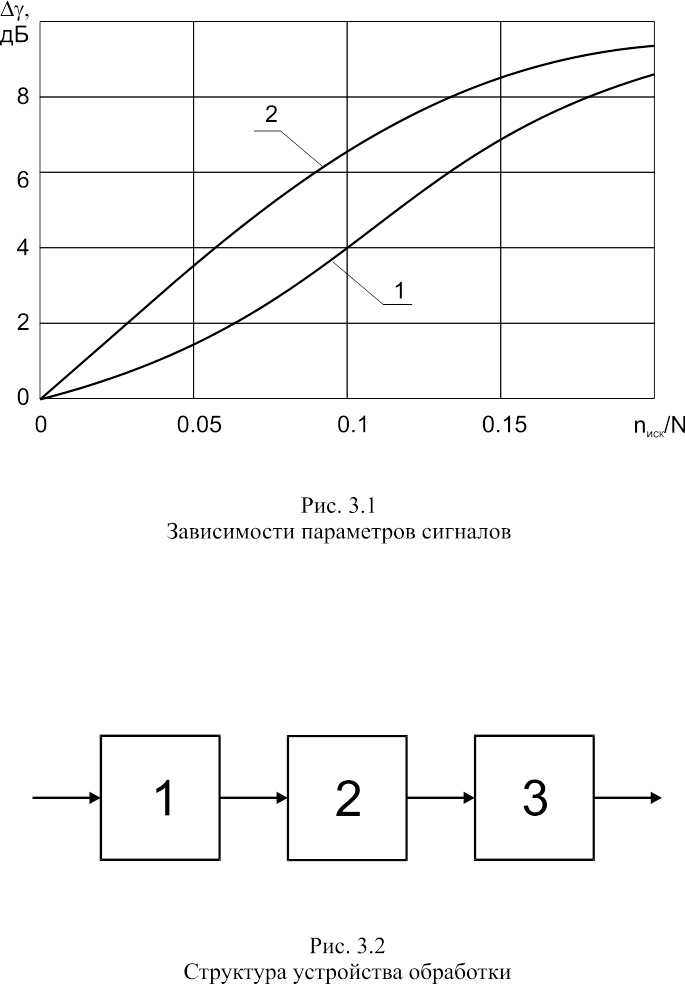
На рис. 3.1 показан график зависимости изменения УБВ Dg АКФ от относительного числа искаженных символов nиск/N для синтезированного сигнала (кривая 1) и М-последовательности (кривая 2) при длине N = 15. Выигрыш в энтропии у синтезированного сигнала составляет порядка 32 %, при этом выигрыш в изменении УБВ достигает 2.5 дБ.

Таким образом, показана возможность синтеза ФМн сигналов, робастных к искажению отдельных символов, на основе критерия максимума удельной энтропии сигнала.

3.3 Синтез фазоманипулированных сигналов на основе составных последовательностей

В настоящее время не существует эффективной методики синтеза последовательностей для ФМн сигналов с базой порядка 500 и выше [34, 35]. С ростом базы растет время синтеза сигнала и фильтра, а выигрыш по сравнению со случайными последовательностями уменьшается.

Поэтому для построения сигналов со сверхбольшими базами применяют либо последовательности со случайным набором символов, либо превосходящие их по своим корреляционным свойствам М-последовательности [34]. В то же время при использовании таких последовательностей не удается получить сигналы с заданными спектральными характеристиками.

Другим перспективным путем синтеза ФМн сигналов с большими базами является использование СП [34], которые можно различными способами получить из известных псевдослучайных последовательностей (ПСП). Первый способ состоит в формировании СП в виде ряда сегментов, каждый из которых представляет собой какую-либо ортогональную (или квазиортогональную) ПСП. Так, в [94] описано построение СП на основе обобщенных дополнительных последовательностей, которые обладают хорошими свойствами автокорреляционной функции (АКФ) в районе главного лепестка. Однако обработка каждого сегмента СП на приемной стороне ведется отдельно от других, что сильно

усложняет устройство обработки, кроме того, совершенно не учитываются спектральные характеристики получаемых СП.

Другой возможный способ формирования СП состоит в модуляции одной ПСП, которая в данном случае называется несущей последовательностью (НП), другой ПСП - модулирующей (МдП). Свойства получаемой СП полностью определяются свойствами НП и МдП, например, доказано, что УБВ получаемой СП не может быть ниже УБВ используемых НП и МдП [35]. Поэтому в качестве НП и МдП используют ПСП с хорошими автокорреляционными свойствами.

Так, для НП обычно [95, 97] применяют бинарные последовательности - коды Баркера и М‑последовательности, а МдП может быть как бинарной [95], так и многомерной, например, четверичной [97]. Общим недостатком указанных подходов является учет только корреляционных свойств СП, что не дает возможность синтезировать сигналы по заданной СПМ, кроме того, для четверичных ПСП необходимо более сложное устройство обработки, т.к. при передаче они представляются в виде двух бинарных.

Напротив, в [93] для синтеза СП на основе многомерной МдП используется только спектральный критерий приближения. Для этого формируют алфавит из применяемых НП, т.е. каждому возможному значению элемента СП ставят в соответствие свою бинарную НП Рида‑Мюллера, которая имеет относительно узкий спектр на заданной частоте. Комбинируя определенные НП, удается получить заданную форму СПМ сигнала. К недостаткам указанного подхода можно отнести низкие корреляционные характеристики получаемых СП, т.к. для синтеза применяется только спектральный критерий приближения.

Другим фактором, сдерживающим применение ФМн сигналов с большими базами, является необходимость построения согласованных фильтров с большим числом элементов памяти, т.е. цифровых фильтров высоких порядков. Таким образом, важно отметить, что при синтезе сигналов необходимо учитывать не только спектральные и корреляционные свойства отдельных сигналов, время их синтеза, но и возможность их эффективной обработки.

Поэтому в большинстве случаев задачу синтеза ФМн сигналов на основе СП необходимо рассматривать как многокритериальную, в которой показатели качества отражают определенные свойства СПМ и АКФ. Как будет показано ниже, использование СП позволяет применять эффективные устройства обработки ФМн сигналов. Время же синтеза СП определяется только временем синтеза НП и МдП, т.е. существенно меньше времени синтеза ПСП такой же длины.