Разработка методов многокритериального синтеза сигналов и устройств обработки, обеспечивающих робастные качественные показатели системы, страница 24

где l34 - коэффициент общего решения однородного уравнения.

Значение коэффициентов l31 - l34 находятся подстановкой выражения (3.29) в функционалы (3.23) - (3.25), а также заданием начальных условий. Исходя из особенностей рассматриваемой задачи, в качестве начальных условий используются следующие равенства m(0) = 1, m(±0.5) = 0 и m¢(±0.5) = 0.

Результаты расчетов [116] таких параметров синтезированной модулирующей функции как энергетические потери rA и полоса частот сигнала DF0.99 по уровню 99 % энергии от значения коэффициента b2 приведены на рис. 3.5

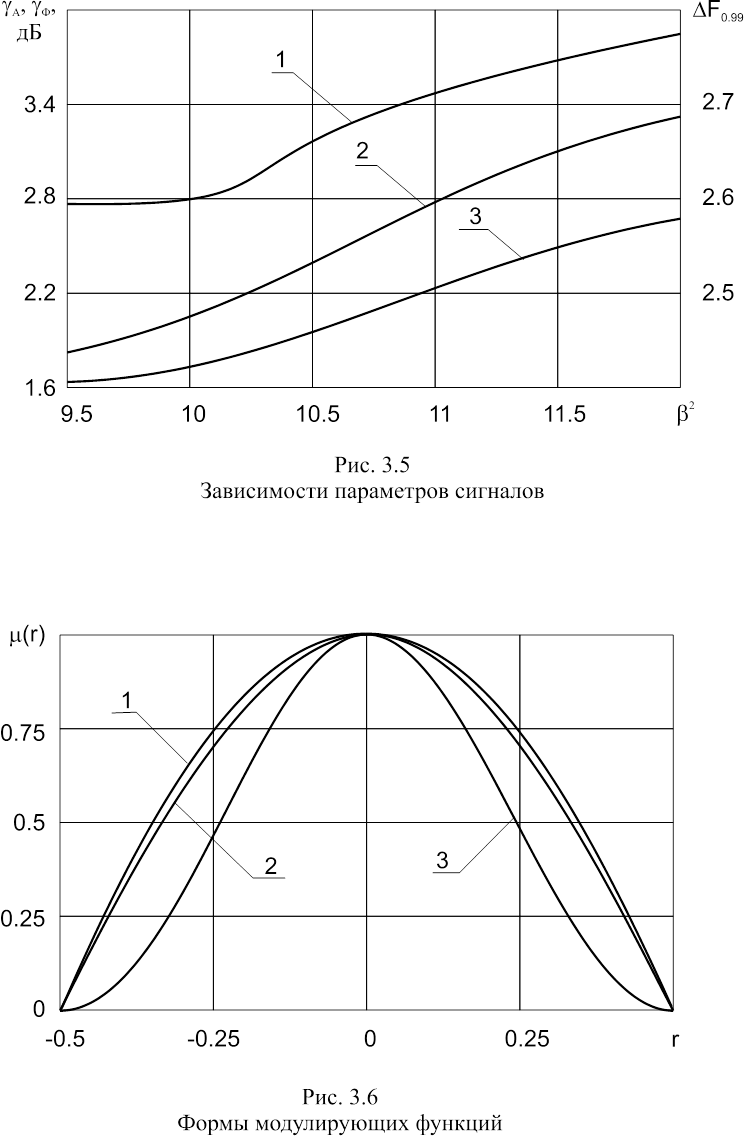
(кривые 1, 2 соответственно). Там же построена зависимость энергетических потерь для фазовых методов ограничения полосы частот [37], возникающих при обработке модулированных ФМн сигналов по сравнению с классическими

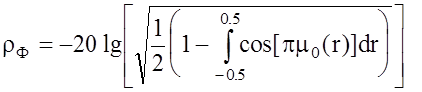                                            (3.30)

(рис. 3.5, кривая 3). Функционал I3(m) обеспечивал во всех рассматриваемых случаях среднюю скорость убывания уровня внеполосных излучений 1/Dw5 [117, 118]. Анализ зависимостей, приведенных на рис. 3.5, показывает, что син-

тезированные модулирующие функции превосходят по всем показателям функцию вида cos2(r), уступая ей только в скорости убывания уровня внеполосных излучений, которая для функции cos2(r) составляет 1/Dw6. Так, выигрыш в величине энергетических потерь в этом случае составляет DrA = 0.7 - 1.4 дБ для амплитудных методов и DrФ = 0.6 ‑ 1.3 дБ для фазовых методов ограничения полосы. При этом сокращение полосы частот по уровню 0.99 энергии сигнала достигает 10 ‑ 13 %.

Сравнение параметров синтезированных модулирующих функций с функциями вида cos(r) показывает [102, 117, 118], что при примерно одинаковой полосе DF0.99, ФМн сигналы с модуляцией отдельных символов по закону m0(r) выигрывают на 0.2 дБ в уровне энергетических потерь как при амплитудных, так и при фазовых методах сокращения полосы. Кроме того, данные сигналы имеют более высокую скорость убывания уровня внеполосных излучений, чем сигналы с модулирующей функцией вида cos (r), для которых она составляет 1/Dw4. На рис. 3.6 (кривая 1) приведена форма синтезированной модулирующей функции m01(r), которая обеспечивала при полосе DF0.99T = 2.5 энергетические потери при обработке DrA = 2.8 дБ, DrФ = 1.7 дБ, там же (кривые 2, 3) построены формы функций модуляции вида cos(r) и cos2(r).

Кроме того, на рис. 3.7 построены, рассчитанные по методике, приведенной в [37], характеристики удельных затрат полосы bF = DF/C и энергии bE = Ed /N0 , где C - пропускная способность каналов связи, Ed - энергия, затраченная для передачи одного бита информации, N0 - спектральная плотность мощности шума для сигналов с модуляцией по законам m01(r), cos(r) и cos2(r) (кривые 1, 2, 3 соответственно). Приводимые кривые [102, 116] позволяют сделать вывод о том, что ФМн сигналы с синтезированной функцией модуляции от дельных символов m01(r) превосходят сигналы с модуляцией по законам cos(r) и cos2(r) по помехоустойчивости.

Таким образом, синтезированная по нескольким показателям качества модулирующая функция отдельных символов ФМн сигналов, позволяет улучшить качественные показатели синтезированных выше робастных сигналов, одновременно повышая их помехоустойчивость.

3.6 Вопросы программно-аппаратной реализации устройства формирования и обработки фазоманипулированных сигналов

3.6.1. Выбор элементной базы для программно-аппаратной реализации устройства формирования и обработки фазоманипулированных сигналов

Выбор элементной базы реализации радиотехнических устройств является важной самостоятельной задачей, т.к. определяет как схемотехнические решения, так и качественные показатели РТС. Развитие современной элементной базы позволяет строить многие радиотехнические устройства на базе одного сиг-

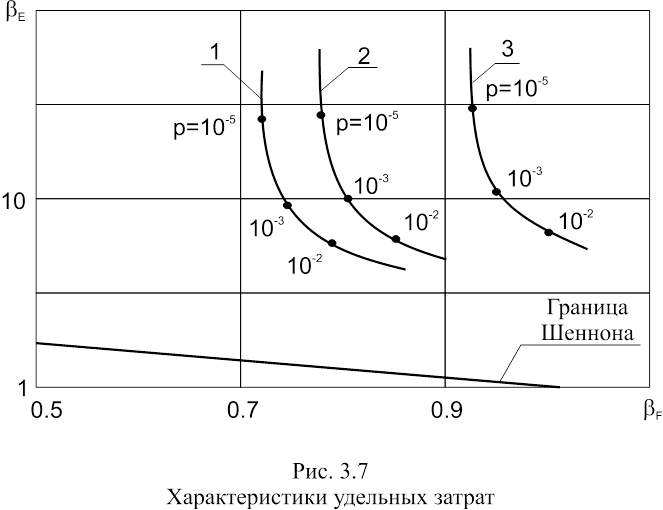
Табл. 3.1. Типовые параметры МП комплектов

Параметр	TMS320C5x	ADSP21xx	DSP5600x
Производительность, MIPS	20	20	16
Число команд	47	51	62
ОЗУ команд	1¸2к ´ 16	1¸2к ´ 16	0.5к ´ 24
ПЗУ команд	2¸4к ´ 16	-	3.75к ´ 24
ОЗУ данных	1к ´ 16	0.5¸1к ´ 16	-
Число последовательных портов	1¸2	2	1
Наличие дополнительных устройств:
АЛУ	+	+	+
МАС	+	+	+
Shifter	+	+	-
HOST-интерфейс	-	+	-

нального (МП) или однокристальной микро-ЭВМ [38, 119]. В этом случае проблема выбора типа МП решается путем формального анализа их параметров. Однако, зачастую, для заданной области применения могут подходить несколько МП, из которых и необходимо сделать выбор. Для таких ситуаций существуют специальные методики выбора МП, описанные, например, в [39, 120].

Как правило, на первом этапе выбора МП по таким показателям как разрядность и форма представления данных определяется несколько подходящих семейств МП [38]. Важно отметить необходимость многокритериального подхода к выбору семейства МП.

Так, с точки зрения разрядности (а следовательно и цены) не рационально использовать 16-разрядный МП, если можно обойтись длиной слова 8 бит. Однако при выполнении отдельных команд, например умножения с накоплением, 16-битный процессор при прочих равных условиях обеспечивает более высокое быстродействие. Как показано в [38], наибольшее распространение в настоящее время получили МП с разрядностями 16, 24 и 32 бита.