Разработка методов многокритериального синтеза сигналов и устройств обработки, обеспечивающих робастные качественные показатели системы, страница 13

Т.к. местоположение ЭЦО определяется фазовыми соотношениями между волнами, приходящими от отдельных светящихся точек, то при изменении ориентации объекта происходит изменение как координат ЭЦО так и амплитуды отраженного сигнала. Как показано в [61], ЭЦО может располагаться не только в пределах габаритных размеров радиолокационного объекта, но и выходить за эти пределы, блуждая в зависимости от направления облучения.

При этом функция неопределенности Вудворда уже не характеризует сигнал на выходе согласованного фильтра, поэтому вводят функцию неопределенности пространственно распределенного объекта [60]. Для фиксированного значения частоты Допплера j ее можно записать в виде

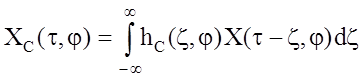,                                                     (2.12)

где C(t, j) - функция неопределенности точечного объекта, а hC(t, j) - импульсная переходная функция распределенного объекта

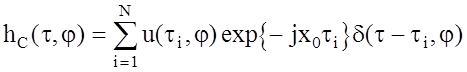                                    (2.13)

где u(ti, j) - амплитуда, соответствующая i-му точечному отражателю, который расположен на расстоянии ti и имеет доплеровскую частоту j, x0 - несущая частота, d(t ‑ ti, j) - дельта-функция.

Таким образом, функция неопределенности распределенного объекта представляет собой семейство переменных во времени зависимостей, имеющих сдвиги по частоте, причем фазовая и амплитудная информация, содержащаяся в приходящем сигнале, сохраняется.

Обнаружение объекта состоящего из N независимых элементов, не флюктуирующих по дальности, подробно рассмотрено в [60]. Предполагалось, что сигнал представляет собой последовательность N импульсов с равномерно распределенными в пределах от 0 до 2p фазами. Время появления импульсов известно. Обнаружение сигнала производилось на фоне нормального белого шума со спектральной плотностью N0. Полагалось, что сигнал обрабатывается в согласованном фильтре. Рассмотрим случай, когда огибающие импульсов полностью некоррелированы, оптимальный приемник представляет собой квадратичный детектор с линейным интегратором [73]

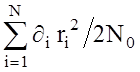^>_< gпор,                                                                               (2.14)

где  - коэффициенты весовой обработки в i‑ом канале, ri2 - отношение сигнал-шум в i-м импульсе, а gпор - порог обнаружения. При этом эффективная поверхность рассеяния e отдельных ЭЦО описывалась с помощью второй модели Сверлинга:

p(e) = 4e×exp{-2e/se}/(se)2, при se > 0,                                                 (2.15)

где se - параметр распределения. В этом случае амплитуда сигналов U на выходе СФ подчиняется распределению Накагами:

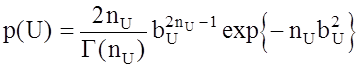.                                                     (2.16)

Здесь nU и bU - параметры распределения, G(m) - гамма-функция.

Однако из-за того, что сигналы на выходе устройства обработки, принимаемые от ЭЦО, имеют колоколообразную форму, под влиянием флуктуаций времени прихода импульсов происходит дополнительное изменение вида закона распределения амплитуды сигнала на выходе СФ.

При отсутствии временных флюктуаций отсчет амплитуды сигнала производится в момент максимума АКФ, поэтому математическое ожидание временных флюктуаций полагаем равным нулю. Дисперсию временных флюктуаций обозначим как sвх2. Статистические характеристики амплитуды сигнала на выходе фильтра, вызванные флюктуацией времени прихода, можно рассчитать как статистические характеристики сигнала на выходе некоторого нелинейного элемента. Вид нелинейной характеристики при этом совпадает с видом АКФ сигнала, а на вход поступает заданный нормальный случайный процесс с нулевым математическим ожиданием и дисперсией sвх2.

Один из возможных методов расчета статистических характеристик сигнала на выходе безынерционного нелинейного элемента приведен в [74]. Обозначим входной процесс как t(t), это нормальный стационарный процесс с нулевым математическим ожиданием и дисперсией sвх2. Амплитуда сигнала на выходе СФ находится по формуле ug(t) = R[t(t)], где R(t) - автокорреляционная функция. Как показано в [74], при линейной аппроксимации R(t) с шагом ht характеристики процесса ug(t) имеют вид 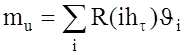, , 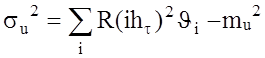а весовые множители Ji находятся по формуле , где D = ht/sвх.

В общем случае, если дополнительно учитываются и флюктуации доплеровской частоты, входной процесс представляет собой двумерный нормальный стационарный процесс с нулевыми математическими ожиданиями и дисперсиями st2 (дисперсия флюктуаций времени прихода импульсов) и sj2 (дисперсия флюктуаций доплеровской частоты).

Характеристика нелинейного элемента совпадает с функцией неопределенности, а статистические характеристики сигнала на выходе устройства обработки рассчитываются по методике, изложенной выше.

В дальнейшем для упрощения вычислений будем полагать, что флюктуации доплеровского сдвига частоты отсутствуют.

С учетом флюктуаций амплитуды результирующий сигнал можно записать в виде U = U1U2, где U1 - множитель, зависящий от энергии отраженного сигнала, т.е. пропорциональный ЭПР, а U2 - масштабный множитель, учитывающий уменьшение амплитуды из-за флюктуаций времени прихода импульсов. Множитель U1 распределен по закону Накагами. Распределение множителя U2 в общем случае неизвестно, но его характеристики можно рассчитать по формулам, приведенным выше. В результате распределение величины U будет отличаться от распределения Накагами и вероятности обнаружения такого сигнала будут зависеть от формы его спектра.

Параметры распределения величины U можно выразить через параметры распределений U1 и U2. Обозначим математическое ожидание флюктуаций величины U1 как mU1, а дисперсию как sU12. Для флюктуаций величины U2 введем соответственно mU2 и sU22.

Случайные величины U1 и U2 независимы [62], их двумерную плотность распределения вероятности p(U1, U2) можно представить в виде p(U1, U2) = p1(U1)p2(U2). Следовательно, математическое ожидание mU = mU1mU2, а дисперсия sU2 = sU12(sU22 ‑ mU22) + mU12.