Для оценки основных параметров синтезированных сигналов были построены
зависимости максимального уровня боковых выбросов АКФ g и нормированной
разрешающей способности по дальности TR от значения коэффици-
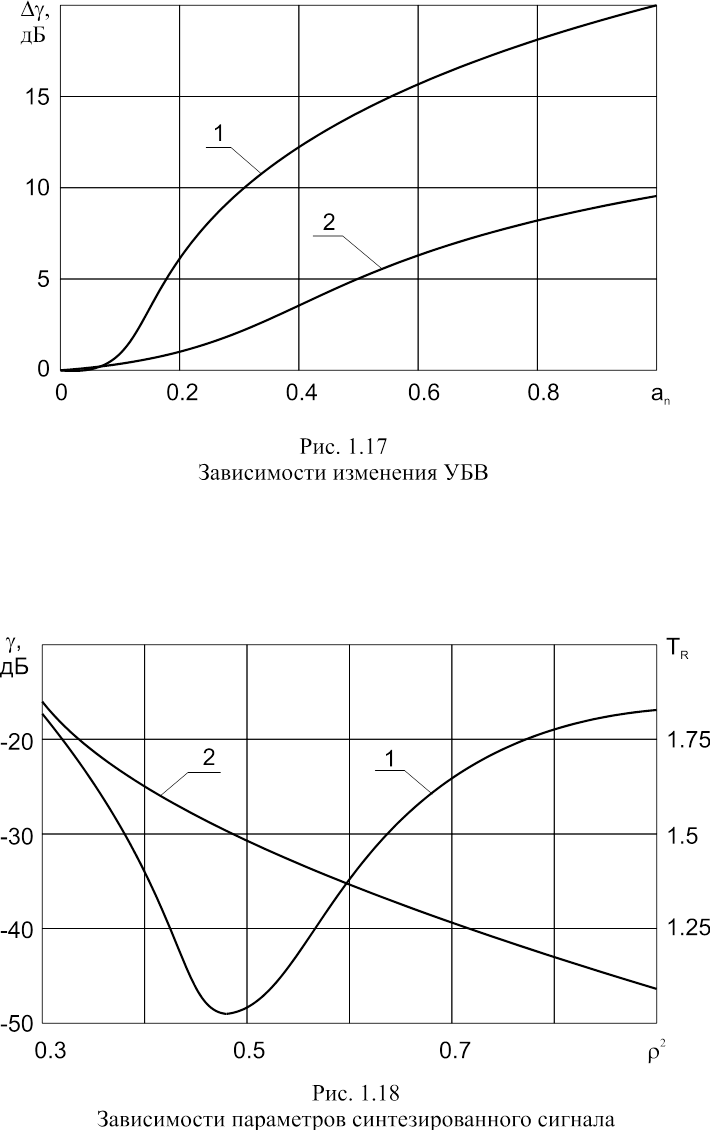
ента частотно-временной связи (рис. 1.18, кривые 1 и 2 соответственно). При увеличении r2 от 0.3 до 0.9 максимальный УБВ изменяется в диапазоне -16 дБ до -49 дБ, а значение TR уменьшается от 1.8 до 1.1. Выражения (1.29) - (1.31) и зависимости, приведенные на рис. 1.18, позволяют, исходя из требований к разрешающей способности, неоднозначности, точности оценки времени запаздывания и доплеровского смещения частоты, выбрать параметры сигнала.
Анализ результатов показывает [53, 54], что сигналы с СПМ GH(x) проигрывают синтезированным сигналам в разрешающей способности на DTR = 14 % и в точности оценки времени запаздывания в 9.8 раза.
Таким образом, решена задача многокритериального синтеза робастных к искажениям сигналов, обеспечивающих при совместных измерениях времени запаздывания и доплеровского смещения частоты сигнала потенциальную разрешающую способность.
Проведенные исследования показали возможность синтеза устройств обработки, робастных к действию мешающих факторов не только на основе статистических подходов Цыпкина и Хьюбера, но и на основе вариационных методов синтеза передаточной функции устройства обработки. Многокритериальный синтез СПМ сигналов позволил обеспечить слабую чувствительность к действию мешающих факторов непосредственно в передаваемых сигналах, что дало возможность применять в качестве робастных устройств СФ.
Анализ результатов исследований позволяет сделать следующие выводы:
1. Информационный критерий максимума удельной энтропии позволяет при наличии минимальной априорной информации о параметрах входного сигнала и уровне искажений синтезировать устройства обработки, робастные к искажению спектра входного сигнала. Показано, что при одинаковом уровне искажений синтезированные устройства обработки превосходят СФ по УБВ сигнала на выходе фильтра на 5‑10 дБ и имеют более слабую зависимость параметров выходного сигнала от уровня искажений.
2. Синтез сигналов на основе критерия максимума удельной энтропии позволил при обработке в СФ получить более слабую чувствительность параметров выходного сигнала к амплитудно- и фазо‑частотным искажениям спектра входного сигнала, чем у сигналов с СПМ GH(x). Кроме того, синтезированные сигналы превосходят сигналы с СПМ G0(x) по уровню удельной энтропии на 10‑30 %, т.е. по своим параметрам приближаются к соответствующим параметрам шума.
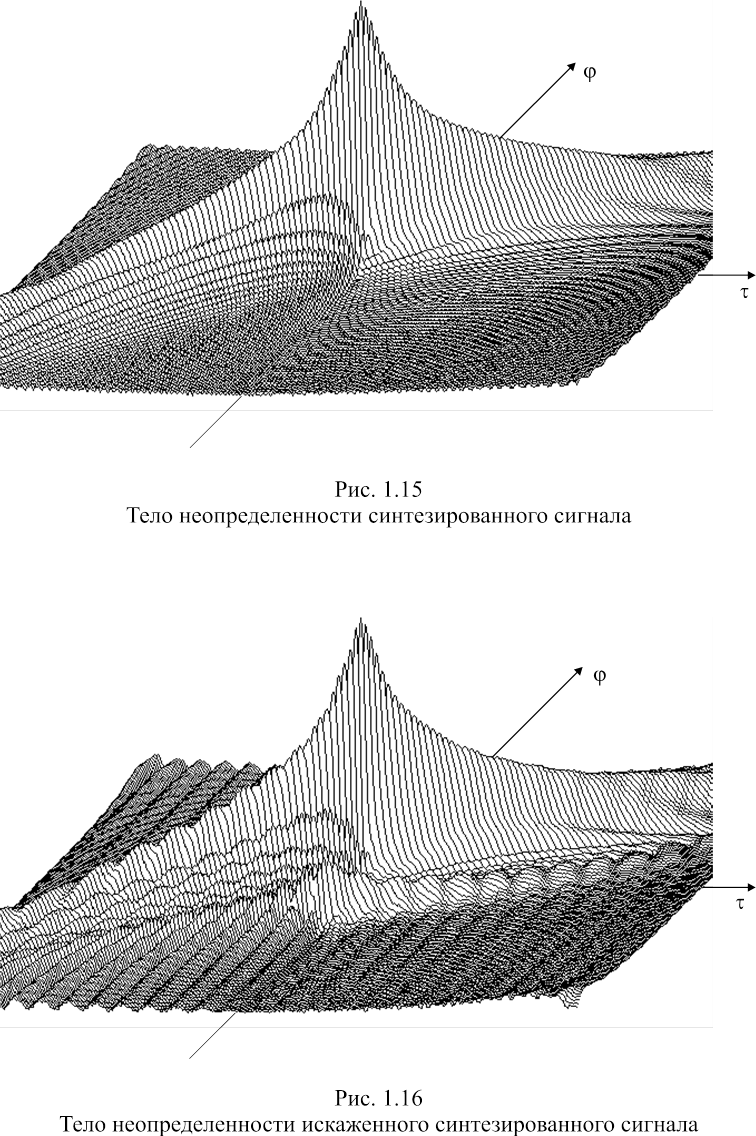
3. Сигналы с высокой скоростью спада основного лепестка тела неопределенности по оси доплеровских частот, что эквивалентно низкому значению коэффициента частотно‑временной связи, позволяют минимизировать влияние амплитудных модуляционных искажений входного сигнала на параметры отклика СФ. Синтез сигналов по данному критерию обеспечил выигрыш в УБВ отклика СФ до 10 дБ по сравнению с сигналами с СПМ GH(x) при одинаковом уровне амплитудных модуляционных искажений.
Таким образом, в первой главе работы рассмотрены вопросы многокритериального синтеза сигналов и устройств обработки, робастных к действию мешающих факторов, введены основные показатели качества и проведен анализ полученных решений.
В первой главе было показано, что при использовании энтропийного критерия качества вариационные методы синтеза позволяют получать обладающие высокими качественными характеристиками сигналы и устройства обработки, робастные к действию мешающих факторов. Данные решения являются потенциально возможными, однако при их практической реализации, как правило, не удается полностью реализовать все заложенные в них свойства [8]. Кроме того, качественные показатели полученных решений начинают сильно зависеть от точности задания исходных данных, причем при заданной точности возможно существование нескольких решений с различными свойствами.
Данные обстоятельства объясняются тем, что многие задачи синтеза относятся к классу некорректно поставленных [28, 55 и др.]. Само определение корректно поставленной задачи математической физики впервые было введено Ж. Адамаром. Задача определения решения z из пространства F по исходным данным u из пространства U называется корректно поставленной на паре метрических пространств (F, U), если выполняются следующие условия [56]:
- для всякого элемента u существует решение z из пространства F;
- решение определяется однозначно;
- задача устойчива на пространствах (F, U).
Всякая задача математической физики, не удовлетворяющая хотя бы одному из этих условий, называется некорректной. В [28] показано, что к некорректно поставленным задачам относится решение интегрального уравнения Фредгольма первого рода
![]() (2.1)
(2.1)
и в частности решение уравнения типа свертки
![]() . (2.2)
. (2.2)
Следовательно, такие задачи как синтез СПМ сигнала по заданной АКФ и синтез сигнала по заданному отклику должны рассматриваться как некорректно поставленные. Действительно, идеальная форма отклика фильтра или АКФ сигнала являются нереализуемыми, следовательно, задача синтеза сводятся к решению уравнений вида (2.1) или (2.2) при неточно заданной правой части. В этой постановке задача часто рассматривается в физике, астрономии и радиоэлектронике [57, 58], как задача восстановления сигнала s(t) по отклику измерительного прибора g(t) при заданной аппаратной функции прибора h(t). Исходя из физического смысла задачи, основным критерием качества является минимум среднеквадратического отклонения отклика g(t) от эталона g0(t) [59].
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.