Разработка методов многокритериального синтеза сигналов и устройств обработки, обеспечивающих робастные качественные показатели системы, страница 5

где K(x) = G(x) = |H(x)|2, H(w) ‑ передаточная функция фильтра, x = (w ‑w0)/Dw - относительная частота.

Введем единственное ограничение на энергетику фильтра в заданной полосе частот Dw

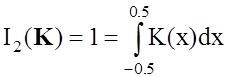.                                                                             (1.3)

Тогда можно сформулировать задачу синтеза робастного фильтра, как задачу поиска экстремума функционала (1.2) при ограничениях (1.3). Это так называемая изопериметрическая задача вариационного исчисления [44], решение которой находится как экстремум вспомогательного функционала

I(K) = I1(K) + l11I2(K),                                                                             (1.4)

где l11 ‑ множитель Лагранжа. Решение уравнения Эйлера-Лагранжа, которое является необходимым условием наличия стационарной точки функционала (1.4) при условии нормировки, равно

K1(x) = rect(x),                                                                                          (1.5)

где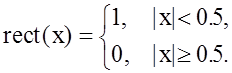

Аналогично можно показать, что огибающая максимально неблагоприятного сигнала равна

u(t) = rect(t), tÎ(-T/2; T/2),                                                                       (1.6)

где T - длительность сигнала. Теперь, полагая, что входной сигнал имеет большую базу и используя метод стационарной фазы [8], можно найти фазовую характеристику фильтра, тем самым завершая синтез робастного устройства обработки сигналов в условиях минимальной априорной информации.

Таким образом, использование показателя качества устройства обработки (1.2) при ограничении только на энергию фильтра в заданной полосе частот Dw приводит к тривиальному решению - фильтру с прямоугольной амплитудно-частотной характеристикой (АЧХ). Как известно такая система не удовлетворяет требованиям по неоднозначности оценки времени запаздывания [8] из-за высокого уровня боковых выбросов (УБВ) отклика фильтра.

Повышения качественных характеристик устройства обработки можно достичь используя дополнительную информацию о принимаемом сигнале. Например, можно учесть, что реальные сигналы, как правило, имеют неравномерный спектр и использовать ограничение на эффективную ширину полосы пропускания 2b фильтра, где

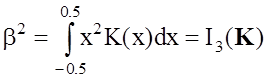.                                                                       (1.7)

В этом случае, вспомогательный функционал (1.4) принимает вид

I(K) = I1(K) + l12I2(K) + l13I3(K),

а решение уравнения Эйлера-Лагранжа равно

.                                            (1.8)

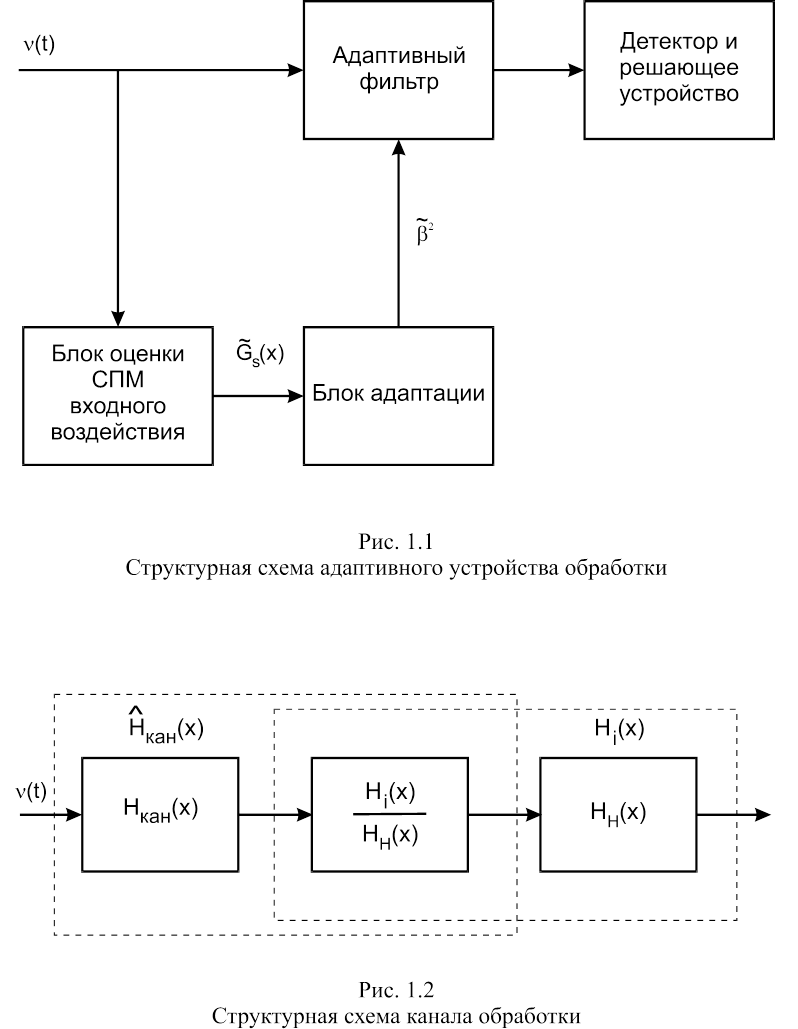
При отсутствии априорной информации об эффективной ширине спектра входного воздействия система должна оценить ее и по этой информации проводить адаптацию фильтра. Соответствующая структурная схема адаптивной системы приведена на рис. 1.1.

На вход системы поступает воздействие n(t) с СПМ Gn(x), представляющее собой смесь искаженного сигнала s(t) и аддитивного шума e(t). Блок оценки СПМ входного воздействия должен на основе какого-либо алгоритма спектрального оценивания сформировать оценку СПМ , необходимую для вычисления оценки , определяющей эффективную ширину спектра полезного сигнала.

В [45] для повышения быстродействия и точности системы при оценке СПМ предлагается использовать многоканальный алгоритм параллельного спектрального оценивания, основанный на ММЭ. При этом для оценивания СПМ  используется M фильтров с передаточными функциями . Тогда значения дисперсий входного воздействия на выходе фильтров равны

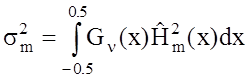.                                                                          (1.9)

За оценку СПМ  принимается функция G(x), максимизирующая энтропию входного воздействия:

,

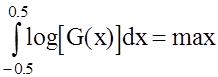при ограничениях (1.9). Такой подход, как показано в [45], обеспечивает скорость оценивания прямо пропорциональную числу каналов. Точность оценивания увеличивается втрое при удвоении числа каналов, а при большом M оценка  совпадает с оценкой по методу максимального правдоподобия.

Блок адаптации на основе оценки СПМ  вырабатывает оценку , в соответствии с которой происходит изменение параметров адаптивного фильтра. Отклик фильтра детектируется и проходит на решающее устройство.

Рассмотрим влияние объема априорной информации о параметрах входных сигналов на характеристики синтезированных устройств обработки. Для упрощения расчетов будем считать канал стационарным со случайной передаточной функцией Hкан(x). Данное ограничение позволяет нагляднее показать влияние формы передаточной функции канала на величину искажений.

В качестве входного сигнала будем использовать широко распространенный в радиолокации сигнал с СПМ вида [8]

G0(x) = k0 + (1 ‑ k0)×cos2(px), xÎ(-0.5; 0.5).                                         (1.10)

При k0 = 0.08 выражение (1.10) описывает сигнал с СПМ Хэмминга GH(x).

Канал обработки сигнала представляет собой последовательно включенные фильтр с передаточной функцией Hкан(x), соответствующий каналу передачи, и устройство обработки с передаточной функцией Hi(x) при i = 1, 2 (рис. 1.2), которая описывается выражениями (1.5), (1.8), или фильтр Hкан(x) и фильтр HH(x), согласованный с входным сигналом. Устройство с характеристикой (1.5) используется, если известна только полоса частот Dw сигнала. В случае дополнительно известной эффективной ширины полосы пропускания 2b, применяется фильтр с характеристикой (1.8), а при полностью известном входном сигнале, применяется СФ HH(x). Представим передаточную функцию устройства обработки в виде

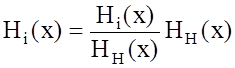
Тогда канал обработки можно представить как последовательное соединение искажающего фильтра (ИФ) с передаточной функцией  и фильтра, согласованного с сигналом Хэмминга HH(x) (рис. 1.2). Таким образом, ИФ учитывает как влияние канала связи, так и отличие устройства обработки от СФ. Теперь анализ влияния искажений на параметры отклика сигнала на выходе устройства обработки можно провести методом парных эхо [8]. Для этого представим частотную характеристику ИФ в виде разложения в ряд Фурье