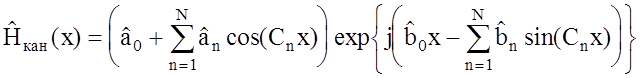Разработка методов многокритериального синтеза сигналов и устройств обработки, обеспечивающих робастные качественные показатели системы, страница 6

,       (1.11)

где , , Cn - коэффициенты разложения в ряд Фурье, N ‑ число членов разложения. Здесь предполагается, что  является функцией с ограниченным спектром, что не противоречит действительности, т.к. полоса пропускания устройства обработки реально ограничена.

Можно показать [8], что при малой величине фазовых ошибок (меньше 0.5 рад) функция отклика СФ на искаженный сигнал будет иметь вид

,

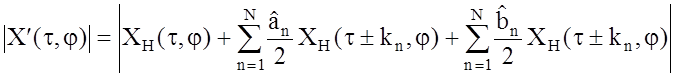где |CH(t, j)| ‑ функция отклика СФ HH(x) на неискаженный сигнал с СПМ GH(x), kn ‑ число полных периодов пульсаций амплитуды или фазы в полосе сигнала, t ‑ время задержки, j ‑ доплеровское смещение частоты. Компоненты, имеющие одинаковый положительный и отрицательный сдвиг по оси времени, в силу своего расположения получили название "парных эхо".

Таким образом, влияние искажений на выходе устройства обработки проявляется в виде суперпозиции функции отклика СФ на неискаженный сигнал и "парных эхо" от всех спектральных компонент передаточной функции ИФ. Следовательно, для анализа искажений достаточно рассмотреть влияние одного члена разложения передаточной функции ИФ на устройство обработки и обобщить полученные результаты на N компонент.

Как следует из анализа рис. 1.2, часть ИФ с передаточной характеристикой , учитывающая отличие применяемого устройства обработки от СФ, вносит искажения определенного уровня в отклик устройства обработки. Уровень этих искажений определяется объемом априорной информации о параметрах входного сигнала: чем больше имеется априорных сведений, тем меньше отличие Hi(x) от HH(x), следовательно, и меньше уровень вносимых искажений. С другой стороны, априорная информация о параметрах канала передачи принципиально не может быть полной. Следовательно, с точки зрения анализа чувствительности синтезированных устройств обработки к действию мешающих факторов, наибольший интерес представляет оценка влияния изменения передаточной функции канала связи на параметры выходного сигнала устройства обработки. Для этого представим передаточную функцию канала связи аналогично (1.11) в виде

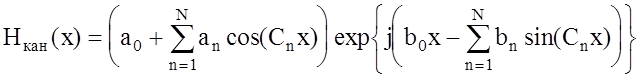
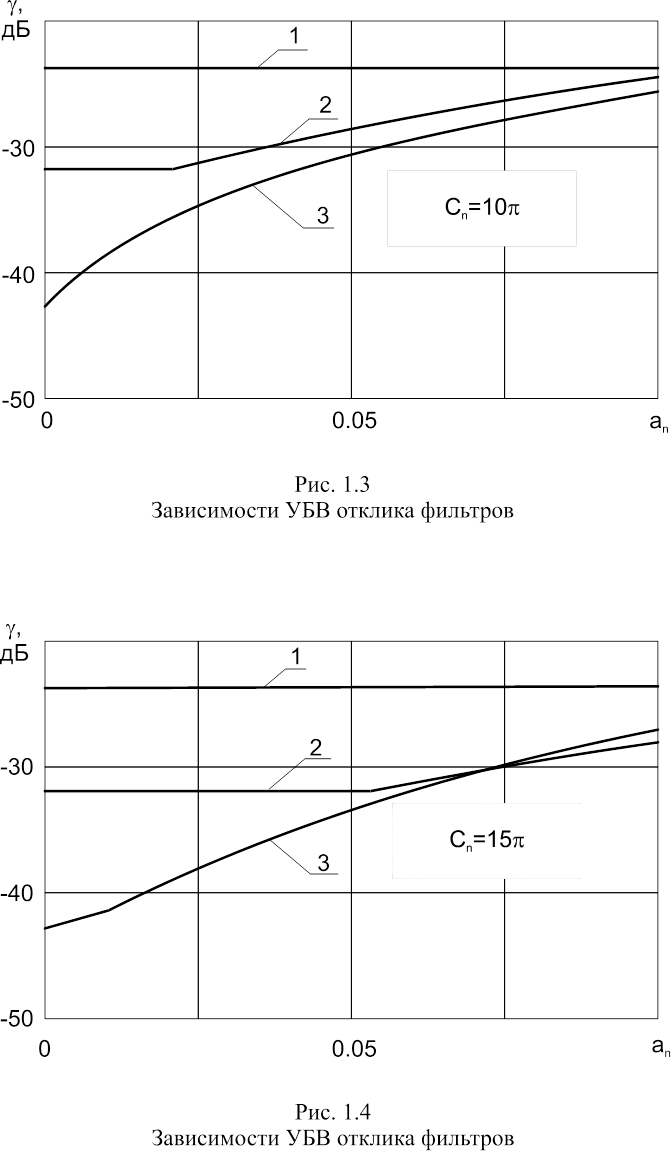
Для анализа характеристик синтезированных устройств обработки были проведены исследования зависимости УБВ g и ширины основного лепестка отклика фильтра по уровню ‑3 дБ от величины амплитудных an и фазовых bn коэффициентов разложения передаточной функции канала связи при различных коэффициентах Cn и большом отношении сигнал-шум. Для примера на рис. 1.3 и 1.4 приведены зависимости g(an) для различных фильтров при Cn = 10p и 15p соответственно. Здесь кривая 1 соответствует фильтру K1(x), кривая 2 - адаптивной системе с фильтром K2(x), а кривая 3 - СФ для сигнала GH(x). В обоих случаях амплитудно-частотные искажения спектра сигнала имели величину пульсаций an, не превышающую 10 % от постоянной составляющей a0.

Анализ приводимых зависимостей позволяет сделать следующие выводы:

1.  Системы с фильтрами K1(x) и K2(x) обладают робастными свойствами при амплитудно-частотных искажениях спектра сигнала в диапазоне до 10 % от уровня постоянной составляющей.

2.  Учет дополнительной информации об эффективной ширине спектра входного воздействия в системе с фильтром K2(x) позволяет получить выигрыш в УБВ порядка 5..10 дБ по сравнению с фильтром K1(x) в диапазоне до 5 % амплитудно-частотных искажений спектра сигнала.

3.  Фильтр K1(x) не чувствителен к амплитудным искажениям, т.к. его УБВ превышает величину парных эхо. Этот вывод является эффектной иллюстрацией синтеза робастного устройства обработки: расчет системы на наихудшую ситуацию приводит к робастному решению, но с низкими показателями качества.

4.  При больших значениях уровня амплитудно-частотных искажений спектра сигнала система с фильтром K2(x) превосходит СФ по УБВ.

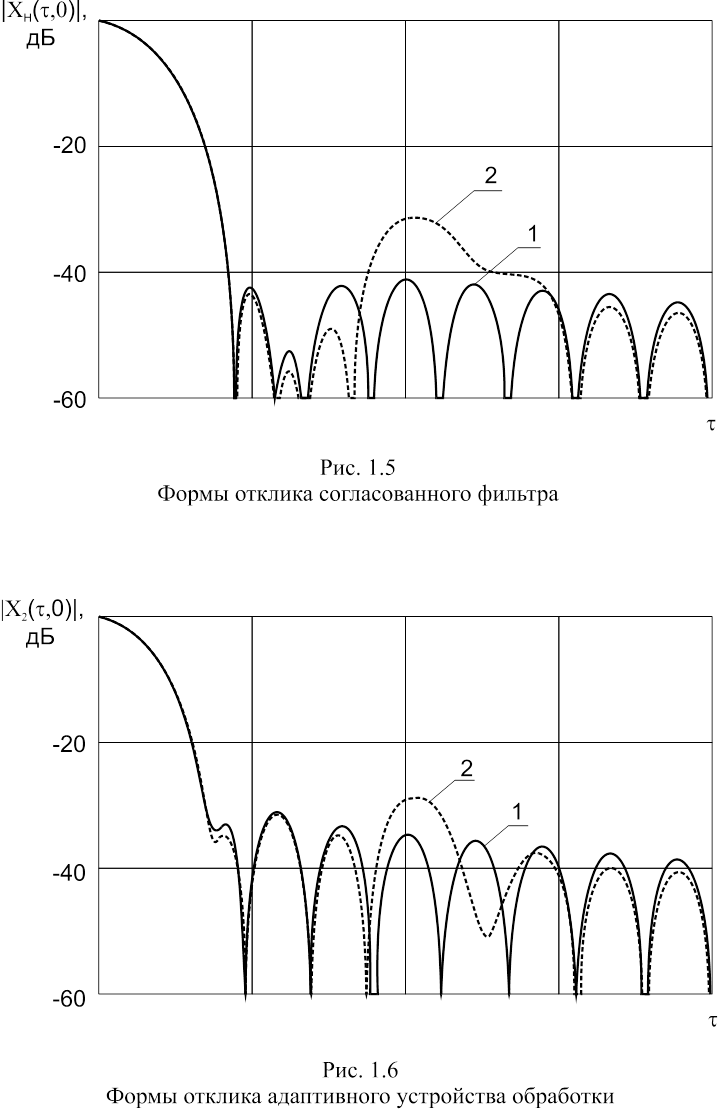
На рис. 1.5 приведены формы отклика СФ |CH(t, 0)| при отсутствии искажений (кривая 1) и при значениях коэффициентов разложения передаточной функции канала связи an = 0.05, Cn = 10p (кривая 2). Аналогичные формы для адаптивной системы |C2(t, 0)| представлены на рис. 1.6. Из приведенных рисунков видно, что система с фильтром K2(x) превосходит СФ с точки зрения робастности УБВ отклика. Кроме того, амплитудные искажения спектра сигнала не приводят к расширению основного лепестка по уровню ‑3 дБ, следовательно, использование синтезированных устройств обработки не приводит к снижению разрешающей способности системы под влиянием амплитудных искажений.

Анализ фазо-частотных искажений спектра сигнала иллюстрируется рис. 1.7, где приведены зависимости УБВ g от уровня искажений bn при Cn = 10p и рис. 1.8, показывающем аналогичные зависимости при Cn = 15p. Здесь кривая 1 соответствует фильтру K1(x), кривая 2 - адаптивной системе с фильтром K2(x), а кривая 3 - СФ для сигнала GH(x). Фазо-частотные искажения исследовались в диапазоне |bn| £ 0.5 рад, при этом УБВ на рис. 1.7 и 1.8 изменяется сильнее, чем при амплитудно-частотных искажениях спектра сигнала. В остальном указанные рисунки позволяют сделать выводы аналогичные выводам по амплитудно-частотным искажениям спектра сигнала.

Обобщая вышесказанное, отметим, что при совместных амплитудных и фазовых искажениях спектра сигнала возможна как частичная компенсация, так и увеличение искажений в зависимости от знаков коэффициентов an и bn. При учете N компонент разложения передаточной функции канала связи и предположении о том, что искажения малы, в отклике получается 2N независимых парных эхо. Следовательно, при N амплитудных и фазовых компонент система останется робастной, т.к. она робастна по любой из независимых компонент. При значительном возрастании уровня искажений в отклике фильтра появляются перекрестные произведения компонент, вызванные амплитудно- и фазо‑час-