Разработка методов многокритериального синтеза сигналов и устройств обработки, обеспечивающих робастные качественные показатели системы, страница 21

Таким образом, синтез МдП по критерию приближения (3.6) позволяет получать СП с хорошими корреляционными свойствами, при простой схеме обработки и низкой чувствительности к искажениям отдельных символов, но при-

водит, по причине поэлементного приема, к потерям в отношении сигнал-шум, зависящим от соотношения длин несущей и модулирующей ПСП [101, 103].

Данный алгоритм синтеза СП можно применять и для синтеза систем сложных сигналов [99, 102, 104]. Задавая различные начальные приближения, (обычно они выбираются по случайному закону) можно получать различные ПСП со схожими свойствами АКФ и СПМ. Приведенный алгоритм синтеза не требует больших временных затрат и легко реализуется на микропроцессорах обработки сигналов, что будет показано ниже [101].

Дополнительного снижения УБВ составной последовательности при некотором увеличении объема требуемой памяти можно добиться, если вместо согласованного фильтра для МдП использовать весовой фильтр сжатия [100, 102].

3.4 Синтез весового фильтра сжатия фазоманипулированных сигналов, робастного к неточному заданию коэффициентов фильтра

Для снижения УБВ отклика устройства обработки на дискретный сигнал в настоящее время широко применяется [36, 92, 96, 105] весовая обработка. В простейшем случае весовую обработку можно реализовать путем умножения сигналов при их формировании на некоторую последовательность с хорошими корреляционными свойствами [36, 105]. Данный способ гарантирует отсутствие энергетических потерь, но может приводить к изменению других свойств синтезируемых сигналов, в частности спектральных. Кроме того, при такой обработке не удается получить сильного снижения УБВ отклика устройства обработки.

Поэтому обычно применяют более эффективные алгоритмы, основанные на обработке сигналов в ВФ сжатия приемного устройства [36, 92, 96]. При этом синтез ВФ сводится к задаче определения коэффициентов ВФ сжатия, расчет которых обычно осуществляется по двум критериям - минимума УБВ сигнала на выходе ВФ и минимума потерь на обработку [36]. К недостаткам данного подхода можно отнести наличие потерь в отношении сигнал-шум, а так же отсутствие учета влияния искажений.

В [8, 36] рассматриваются типичные для РТС искажения ФМн сигнала, вызванные недостаточной точностью установки фазы манипуляции сигнала и значений коэффициентов ВФ. Кроме того, возможны искажения, связанные с неидеальностью амплитудно-частотной характеристики приемно-передающего тракта, отличием формы модулирующего импульса от прямоугольной и др. Как показано в [36] влияние таких искажений сказывается в значительном увеличении УБВ сигнала на выходе ВФ сжатия и потерь на рассогласование.

Исходя из вышесказанного, задача синтеза коэффициентов ВФ сжатия ФМн сигнала должна ставиться как многокритериальная с учетом влияния искажений.

Представим сигнал на выходе ВФ в виде [37]

                          (3.10)

где  - вектор коэффициентов ВФ, M - порядок ВФ, D = {di}, di = ± 1,  - дискретная последовательность, соответствующая ФМн сигналу s(t). В частном случае, при {h} = {d} выражение (3.10) описывает сигнал на выходе СФ.

Выражение (3.10) можно записать в матричном виде

ADHW = g,                                                                                                (3.11)

где g = (g1, g2, ..., gM+N-1)T - вектор, описывающий выходной сигнал ВФ сжатия, а матица AD имеет вид

.

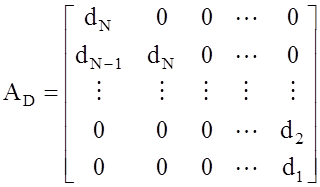Система линейных уравнений (3.11) имеет M + N - 1 уравнений и M неизвестных. На практике порядок ВФ составляет M = (2¸3)N, т.е. число уравнений больше числа неизвестных. В зависимости от соотношения ранга матрицы AD rang(AD) и ранга расширенной матицы rang(AD | g) система (3.11) может иметь одно или несколько решений, а также быть неразрешимой.

Рассмотрим случай единственного решения, т.е. когда rang(AD) = rang(AD | g) = M. Заданная форма отклика ВФ сжатия определяется из требований минимизации УБВ отклика фильтра

g = |gбок|/|gmax|,                                                                                          (3.12)

и потерь на рассогласование

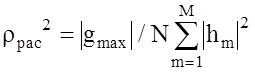                                                                        (3.13)

где |gmax| - центральный пик сигнала на выходе ВФ, |gбок| - уровень максимального бокового выброса.

Необходимо отметить, что в общем случае для заданной последовательности D вид функции g(t) может не соответствовать требованиям практической реализации ВФ. Следовательно, функцию g(t), определяющую заданные g и rрас2, необходимо рассматривать как известную с некоторой погрешностью d

||g(t) - gd(t)|| £ d.                                                                                       (3.14)

Согласно [28], решением уравнения

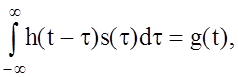                                                                           (3.15)

конечномерным вариантом которого является система (3.11), не может являться решение h(t) уравнения (3.15), т.к. вследствие (3.14) такое решение может не обладать свойствами устойчивости к малым отклонениям g(t).

Исходя из вышесказанного, задачу синтеза ВФ сжатия, устойчивого к влиянию искажений, необходимо рассматривать как некорректно поставленную. Используя для решения системы (3.11) метод регуляризации А.Н. Тихонова, представим задачу синтеза коэффициентов ВФ в виде задачи минимизации вспомогательного функционала

Ma[HW, gd] = FW(HW) + aW[HW],                                                     (3.16)

где , gd - вектор, соответствующий идеализированному отклику ВФ, заданному с погрешностью, a - параметр регуляризации, W[HW] - стабилизирующий функционал.