Разработка методов многокритериального синтеза сигналов и устройств обработки, обеспечивающих робастные качественные показатели системы, страница 12

Критерий максимума отношения сигнал-шум, при известных спектре сигнала S(x) и СПМ помехи N0(x), можно выразить как в явном виде

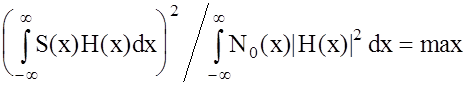,                                      (2.3)

так и через идеальную форму отклика фильтра g0(t)

,                                                                         (2.4)

где H(x) ‑ передаточная функция синтезируемого фильтра, - норма в некотором метрическом пространстве. Последний способ удобнее, т.к. позволяет учесть дополнительные требования на УБВ отклика фильтра, но приводит к некорректной задаче [28] из-за необходимости решения уравнения свертки (2.2).

Поэтому для решения задачи синтеза передаточной функции фильтра, максимизирующего отношение сигнал-шум на выходе при заданных форме и УБВ отклика, воспользуемся методом регуляризации А.Н. Тихонова. В соответствии с данным методом [55] сформируем некоторый вспомогательный функционал вида

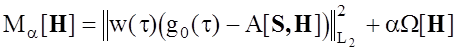,                                       (2.5)

где ‑ квадрат нормы в пространстве L2, w(t) ‑ весовая функция, определяющая влияние величины УБВ отклика фильтра на значение невязки 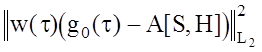, A[S, H] ‑ оператор, связывающий передаточную функцию фильтра H(x) с откликом сигнала на его выходе g(t) (в рассматриваемом случае данный оператор имеет вид 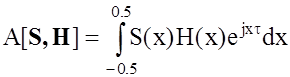), a ‑ параметр регуляризации, W[H] ‑ стабилизатор, вид которого зависит от специфики решаемой задачи.

В общем случае вид стабилизатора определяется выражением [28]

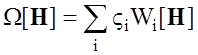,                                                                                  (2.6)

где Vi ‑ весовые множители, Wi[H] ‑ функционалы, ограничивающие отдельные характеристики синтезируемого фильтра.

Исходя из специфики решаемой задачи [64], зададим функционалы Wi[H] в виде

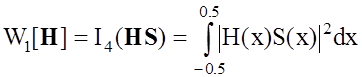,                                                       (2.7)

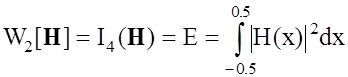,                                                         (2.8)

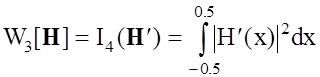.                                                              (2.9)

Здесь выражение (2.7) определяет разрешающую способность сигнала на выходе фильтра, выражение (2.8) - ограничивает энергию фильтра, а выражение (2.9) - накладывает ограничения на гладкость синтезируемой передаточной функции. Как показано в [28], квадратичная форма функционалов Wi[H] гарантирует, что стабилизатор W[H] удовлетворяет всем предъявляемым к нему требованиям.

Для получения решения в аналитическом виде перейдем к конечно‑разностной аппроксимации функционала (2.5) [55].

Ma[H] = (R0 ‑ SeH)T(R0 ‑ SeH) ‑ aHT(V1BTBhx + V2Jhx + V3F2/hx)H,   (2.10)

где  ‑ вектор‑столбец отсчетов передаточной функции фильтра,  ‑ вектор‑столбец отсчетов идеализированного отклика фильтра,  ‑ матрица, определяющая ядро оператора A[S, H], , hx и ht ‑ шаги дискретизации по частоте и времени задержки соответственно, B ‑ матрица, определяющая ядро функционала (2.7)

,

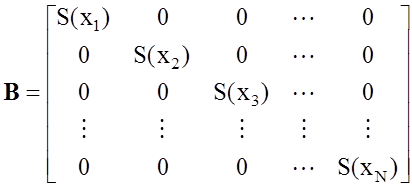J ‑ единичная матрица, F2 = F×FT- матрица, учитывающая конечно-разностную аппроксимацию квадрата первой производной

.

Выражение (2.10) позволяет получить выражение для H(x) в явном виде [65]

H = (SeTSeht + a[V1BTBhx + V2Jhx + V3F2/hx])-1SeTR0.                           (2.11)

Выбор параметра регуляризации a осуществляется на основе метода обобщенной невязки [55]

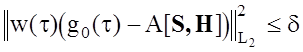,                                                               (2.12)

где d - точность задания исходных данных.

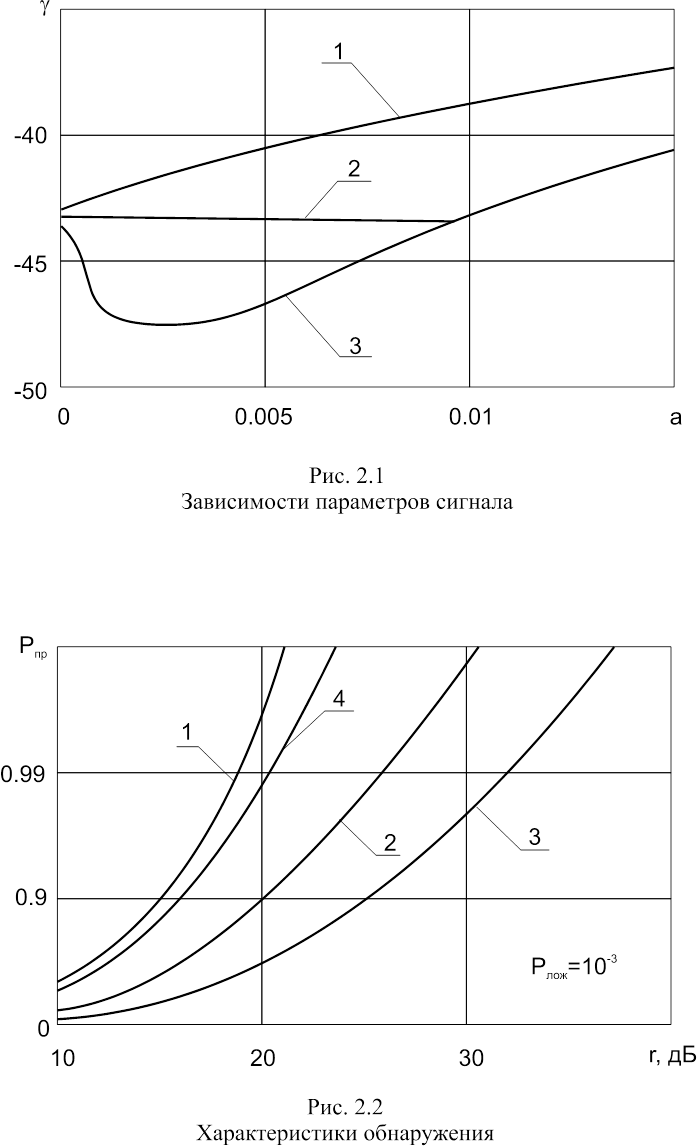
Для анализа полученного решения (2.11) были проведены исследования (аналогично разделу 1.2) зависимости УБВ отклика фильтра от величины амплитудных an коэффициентов разложения передаточной функции канала связи при различных коэффициентах Cn и отношении сигнал-шум q = 10. Для примера на рис. 2.1 приведены зависимости g(an) для синтезированного фильтра при Cn = 10p и входном сигнале с СПМ GH(x). Здесь кривая 1 соответствует СФ для сигнала с СПМ GH(x), кривая 2 - синтезированному фильтру при V3 = 0.2, а кривая 3 - синтезированному фильтру при V3 = 0.12. В обоих случаях синтезированный фильтр практически не проигрывал СФ в отношении сигнал-шум. Некоторый выигрыш в качественных показателях (рис. 2.1, кривая 3) объясняется тем, что робастные системы (согласно моделям Хьюбера и Цыпкина) настроены на входной сигнал с учетом некоторых искажений [21, 22], поэтому при определенных условиях данные системы могут работать лучше, чем при отсутствии искажений.

Из анализа рис. 2.1 можно сделать вывод [66, 67], что использование метода регуляризации для синтеза передаточной функции фильтра позволяет получать устойчивые к неточности задания исходных данных решения, робастные к влиянию амплитудно-частотных искажений СПМ входного сигнала.

2.3. Регуляризация решений задачи синтеза сигналов, обеспечивающих устойчивые характеристики обнаружения пространственно распределенных объектов

Значительное число радиолокационных объектов не могут считаться точечными и должны рассматриваться с учетом их пространственной протяженности. Традиционно [68] под пространственно распределенным объектом понимается тело, геометрические размеры которого значительно превышают размеры элемента разрешения по времени. Однако как показано в [69,…, 71], более правильно считать пространственно распределенным объект, у которого нельзя пренебречь так называемым пространственным шумом, приводящим к ошибкам, которые возникают в радиолокационной системе под влиянием протяженности объекта. Наибольший вклад в пространственный шум вносят так называемые флюктуации местоположения эффективных центров отражения (ЭЦО) объекта [72]. При этом интенсивность результирующего поля в точке приема, создаваемого в какой-либо момент времени, определяется только теми светящимися точками, которые расположены внутри одного разрешаемого объема пространства.