Разработка методов многокритериального синтеза сигналов и устройств обработки, обеспечивающих робастные качественные показатели системы, страница 22

В случае a = 0 рассматриваемая задача сводится к задаче минимизации квадратичного функционала FW[HW], как критерия близости гипотетической функции gd и синтезируемой. В данной постановке рассматриваемая задача совпадает с известными методами синтеза ВФ, которые обеспечивают минимальные значения выражений (3.12) и (3.13), но, как было отмечено выше, не гарантируют устойчивости характеристик искомых решений. При этом для получения устойчивых к искажениям коэффициентов ВФ необходимо сузить пространство возможных решений. Данную функцию в (3.16) выполняет стабилизирующий функционал W[HW], который осуществляет выделение некоторого компактного множества Hком, на котором решение HW Î Hком существует, единственно и устойчиво.

В простейшем случае стабилизирующий функционал вносит ограничения только на энергетику фильтра

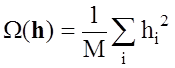,                                                                                    (3.17)

что можно представить в матричном виде как , где J - единичная матрица.

Матричная форма записи функционала (3.16) позволяет получить регуляризованное решение в явном виде [57, 58, 65]

HW = [FWTFW + aJ]-1FWTgd.                                                          (3.18)

Значение параметра регуляризации a находится из уравнения обобщенной невязки [28]

                                                                             (3.19)

Форма идеализированного отклика gd задавалась в виде единичного импульса с заданным УБВ [106, 107].

Для анализа полученных результатов [106,…, 111] проведем сравнение параметров сигналов на выходе синтезированного по критерию (3.16) фильтра сжатия ФМн сигнала и ВФ, рассмотренных в работах [36, 96]. Согласно [36] для 13-элементного кода Баркера, обработанного в ВФ сжатия, имеющего порядок M = 33, обеспечиваются следующие характеристики выходного сигнала: g = ‑29.3 дБ, rрас2 = ‑0.19 дБ. Использование ВФ того же порядка , синтезированного по предложенной выше методике, позволило получить УБВ сжатого сигнала g = ‑32.5 дБ и rрас2 = ‑0.20 дБ.

В работе [96] для 10-ти элементного сигнала D0 = {‑1, 1, ‑1, 1, ‑1, ‑1, 1, 1, 1, 1} рассматривается 12-ти элементный фильтр, обеспечивающий УБВ g = ‑20.83 дБ и потери на рассогласование rрас2 = ‑2.6 дБ. Для тех же исходных данных, синтезированный ВФ [109, 112, 113] сжатия  сигнала D0, синтезированный согласно (3.16) имеет следующие характеристики g = ‑20.91 дБ и rрас2 = ‑1.4 дБ.

Анализ устойчивости синтезированных ВФ сжатия к неточному заданию коэффициентов фильтра проводился методом имитационного моделирования. Для этой цели производилось случайное изменение значений коэффициентов ВФ по формуле

                                                                                             (3.20)

где ej - нормально распределенная помеха с нулевым математическим ожиданием и дисперсией

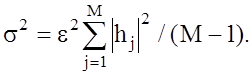
Результаты расчетов [102, 108, 110], иллюстрирующих устойчивость синтезированных по приведенной методике ВФ для 13-элементного кода Баркера, приведены на рис. 3.4. Кривые 1, 2 соответствуют зависимостям УБВ g сигнала на выходе фильтра и потерь на рассогласование rрас2 от значения e для ВФ сжатия, полученного при a = 0, а кривые 3, 4 - фильтру . Из анализа рисунка следует, что искажения коэффициентов ВФ в пределах 5 % от номинальных значений приводит при примерно одинаковых потерях на рассогласование на 2 дБ меньшему возрастанию УБВ в случае расчетов, проведенных по предложенной методике, по сравнению со случаем a = 0. Зависимости на рис. 3.4 позволяют задать требования к допустимому уровню искажений коэффициентов фильтра [102, 111].

3.5 Многокритериальный синтез огибающей символов фазоманипулированных сигналов

Как было отмечено выше, практическое использование дискретных сигналов ограничивается их широкополосностью и низкой скоростью спада уровня внеполосных излучений. При этом влияние амплитудно-частотных и фазо-частотных искажений на свойства ФМн сигналов проявляется в большей полосе частот. В то же время в современных РТС вопросы сужения занимаемой полосы частот и повышения скорости спада уровня внеполосных излучений являются одними из важнейших из-за дефицита радиочастотного ресурса и повышения требований по электромагнитной совместимости.

Решение задачи снижения полосы занимаемых частот и уровня внеполосных излучений возможно различными методами [37, 93 и др.]. Так, в [93] предлагается синтезировать сигналы, энергия которых сосредоточена в заданной полосе частот. Однако, как было показано, данный метод не учитывает корреляционные критерии качества сигналов и, кроме того, синтез всего сигнала для снижения полосы занимаемых частот и уровня внеполосных излучений накладывает серьезные ограничения на вид получаемых ФМн сигналов.

Гораздо большей гибкостью обладают методы, основанные на использовании других видов модуляции: многофазной ФМн (МФМ) и разновидности частотной манипуляции (ЧМн) без разрыва фазы, известной как манипуляция с минимальным сдвигом (ММС). Последний вид модуляции широко применяется в системах подвижной связи [114], где используются сигналы с квадратурной ФМн со сдвигом (p/4 DQPSK) и сигналы с гауссовской ЧМн с минимальным частотным сдвигом (GMSK).

Основным недостатком МФМ сигналов является [37] низкая помехоустойчивость, что сильно сдерживает их применение. Напротив, по своей помехоустойчивости ММС сигналы близки к классическим ФМн сигналам [37], но для этого необходимо в устройстве обработки использовать эффект межсимвольной фазовой связи [37, 114], что приводит к значительному усложнению приемной части системы.