Таким образом, синтезированные сигналы обеспечивают более высокое значение удельной энтропии по сравнению с сигналами с СПМ G0(x) в диапазоне УБВ g = -(35 ¸ 39) дБ при примерно таких же значениях разрешающей способности и точности оценки времени запаздывания.
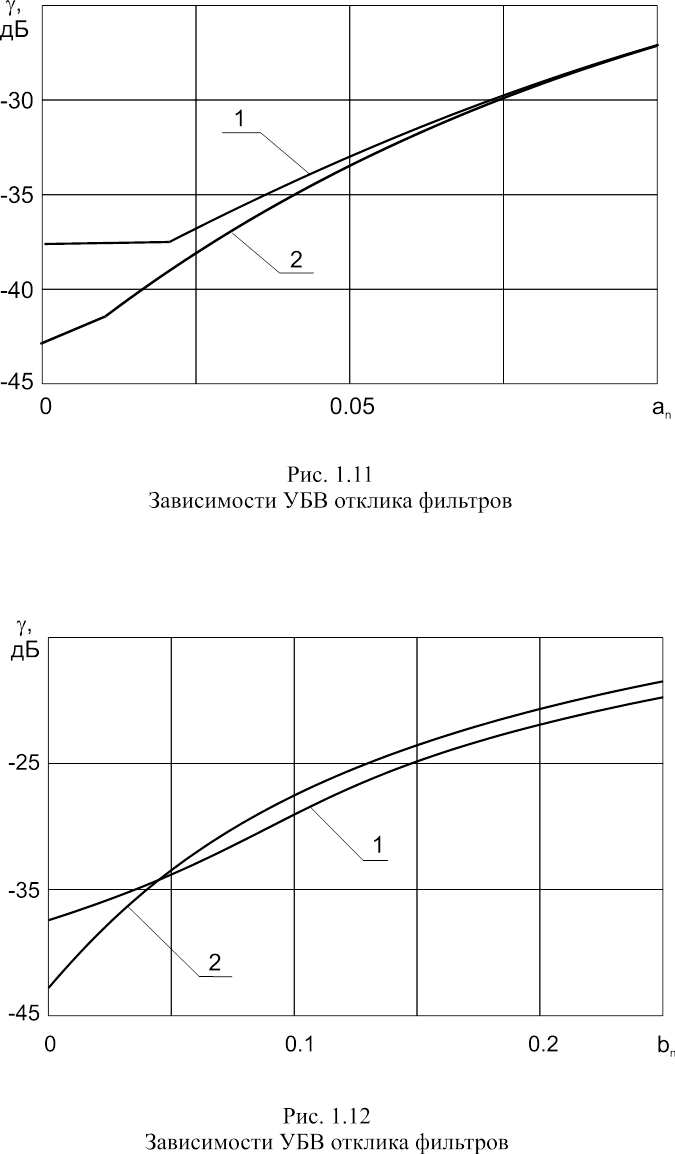
Анализ чувствительности устройств обработки синтезированных сигналов к амплитудно-частотным и фазо-частотным искажениям СПМ проводился по методике, аналогичной рассмотренной выше. Результаты анализа представлены на рис. 1.11, где приведены зависимости УБВ от уровня амплитудно-частотных искажений an спектра сигнала при Cn = 15p, а на рис. 1.12 приведены зависимости УБВ от уровня фазо-частотных искажений bn спектра сигнала при Cn = 15p. На обоих графиках кривая 1 соответствует СФ для сигнала с СПМ G1(x), а кривая 2 ‑ СФ для сигнала с СПМ GH(x).
Из приводимых графиков рис. 1.11, 1.12 можно сделать вывод [50], что использование критерия (1.14) при синтезе сигналов привело к повышению качественных показателей устройств обработки при наличии искажений. В этом случае сигналы с СПМ G1(x) проявляли более слабую чувствительность как к амплитудно‑частотным, так и к фазо-частотным искажениям спектра сигнала, чем сигналы с СПМ GH(x).
Наиболее общей моделью канала со случайными параметрами является канал с частотными и временными селективными замираниями или линейный стохастический канал [51]. Выходной сигнал такого канала описывается выражением
,
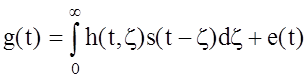где h(t, z) ‑ случайная импульсная характеристика канала в момент времени t на воздействие, поданное в момент t ‑ z, s(t) ‑ входной сигнал, e(t) ‑ аддитивная помеха.
Однако при всей своей общности, данная модель не отражает специфики использования сложных сигналов в многолучевых каналах связи. В данном случае для борьбы с замираниями часто используют отдельную обработку сигналов, пришедших по различным путям распространения [52]. Поэтому более удобной следует считать структурную модель, соответствующую реальному механизму многолучевого распространения сигналов в средах со случайно изменяющимися физическими свойствами [18]. Выходной сигнал такого канала имеет вид
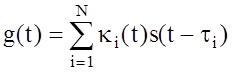, (1.17)
где i ‑ номер луча распространения, N ‑ число лучей, формирующих выходной сигнал, ki(t) ‑ множитель, соответствующий амплитудному преобразованию сигнала в i‑м луче, ti ‑ время запаздывания сигнала в i‑м луче.
Физическая природа множителей ki(t) различна. Например, для коротковолнового ионосферного канала они определяют преобразование сигнала при его отражении от слоев ионосферы и земной поверхности [18].
Кроме многолучевых каналов связи модель (1.17) описывает также радиолокационный сигнал, отраженный от пространственно распределенного объекта [19]. В этом случае множители ki(t) определяют преобразование сигнала при его отражениях от флюктуирующих блестящих точек пространственно распределенного объекта.
В общем случае ki(t) ¹ const в течение длительности сигнала. Особенно сильно это проявляется при использовании сигналов с большой базой для радиолокации пространственно распределенных объектов. Здесь в течение длительности сигнала могут существенно меняться как модуль, так и фаза множителей ki(t), т.е. появляются так называемые модуляционные искажения сигнала [8].
Другим источником амплитудных и фазовых модуляционных искажений являются неизбежные погрешности, возникающие при изготовлении и эксплуатации РТС [8]: несогласованность каскадов, изменение коэффициента усиления во времени, нелинейность модуляционной характеристики и т.п.
При небольших уровнях модуляционных искажений их анализ можно проводить при помощи рассмотренного выше метода парных эхо. Для этого, рассматривая искажающую функцию ki(t), как ограниченную по частоте, можно разложить ее в ряд Фурье аналогично (1.11). Тогда искаженную функцию отклика СФ можно представить в виде
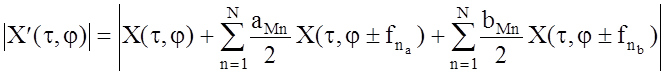, (1.18)
где |C(t, j)| ‑ функция отклика СФ на неискаженный сигнал, aMn и bMn ‑ величины
n‑ых
компонент амплитудной и фазовой модуляции соответственно, 
‑ частоты n‑ых
компонент амплитудной и фазовой модуляции соответственно, j ‑ доплеровский
сдвиг частоты.
В случае измерения только времени запаздывания выражение (1.18) переходит в
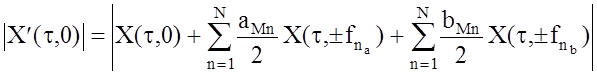. (1.19)
Следовательно, на неоднозначность оценки времени запаздывания оказывает
существенное влияние вид сечения отклика СФ при доплеровских сдвигах 
.
Для примера, на рис. 1.13 приведен отклик СФ на неискаженный
сигнал с СПМ Хэмминга GH(x) при базе 200. Этот график имеет "ножевидную"
форму, т.е. имеет невысокую скорость спада основного лепестка по координате j.
В данном случае амплитудные модуляционные искажения с параметрами aMn = 0.5
и 
приводят к трансформации тела
неопределенности, которая показана на рис. 1.14. Видно, что медленно
спадающий основной лепесток парных эхо создает боковые выбросы на сечении тела
неопределенности при нулевом доплеровском сдвиге. Следовательно, чтобы при
измерении только времени запаздывания модуляционные искажения не оказывали
влияния на сигнал, он должен иметь "кнопочное" тело неопределенности,
т.е. состоящее из единственного пика, окруженного однородно низким пьедесталом.
Как показано
в [8], такие сигналы должны обладать низким значением так называемого коэффициента частотно-временной связи.
Как было показано выше, сигнал, слабо чувствительный к модуляционным искажениям, должен обеспечивать максимальную скорость спада основного лепестка отклика СФ при наличии доплеровского сдвига. Данное требование косвенно связано с требованием минимизации так называемого коэффициента частотно-временной связи [8], определяемого соотношением
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.