Одним из вариантов подхода на основе критериев приближения является синтез дискретного сигнала, максимально приближающегося по своим параметрам к известному аналоговому сигналу с потенциальными значениями показателей качества [33]. Получаемые при этом сигналы в некоторой степени уступают аналоговым эталонам по основным показателям качества, но, с другой стороны, обладают всеми преимуществами дискретных сигналов.
Данный подход позволяет применить методы синтеза аналоговых сигналов и устройств обработки, робастных к действию мешающих факторов при синтезе дискретных сигналов. В этом случае использование информационного критерия максимума удельной энтропии позволяет наложить дополнительные ограничения на СПМ синтезируемых сигналов с точки зрения повышения их робастности к действию мешающих факторов.
Одним из ограничений для синтеза ФМн сигналов с базой более 200 является время синтеза: иногда оно растет пропорционально квадрату длины последовательности. Кроме того, синтез сигналов с базой более 1000, как правило, не дает преимуществ перед использованием М-последовательностей. Одним из возможных методов преодоления указанных трудностей является использование ФМн сигналов на основе составных последовательностей (СП) [34, 94, 95]. Как будет показано в разделе 3.3, использование СП позволяет применять эффективные устройства обработки, снижающие чувствительность параметров отклика СФ к искажению отдельных импульсов входного сигнала.
Однако практическое использование ФМн сигналов с СПМ максимально приближенной к прямоугольной затрудняется низкой скоростью спада уровня внеполосных излучений. При этом влияние амплитудно-частотных и фазо-частотных искажений на свойства ФМн сигналов проявляется в большей полосе частот. Для уменьшения требуемой полосы частот тракта передачи обычно применяют амплитудные и/или фазовые методы [37], основанные на плавном изменении амплитуды огибающей и/или фазы отдельных символов в моменты перескока фазы. Использование указанных методов сопровождается потерями в отношении сигнал-шум. Таким образом, возникает задача синтеза формы модулирующей функции ФМн сигналов, обеспечивающей минимальные потери на обработку при фиксированной скорости спада уровня внеполосных излучений.
Другим ограничением, сдерживающим практическое применение ФМн сигналов является высокий УБВ отклика СФ. Данная проблема особенно актуальна при синтезе сигналов по многим показателям качества и при использовании ФМн сигналов на основе СП. Для снижения УБВ отклика СФ обычно применяют обработку сигналов в весовом фильтре (ВФ) сжатия [36, 96]. При этом требуется обеспечить быстрый расчет коэффициентов ВФ с минимальными потерями на обработку конкретного ФМн сигнала. Однако как будет показано в разделе 3.4, задача синтеза ВФ сжатия ФМн сигналов является некорректно поставленной и получающиеся решения существенно зависят от точности задания исходных данных. Эти обстоятельства обуславливают применение регуляризирующих алгоритмов для синтеза ВФ сжатия робастных к неточному заданию коэффициентов фильтра.
Решение задачи формирования и обработки ФМн сигналов необходимо осуществлять с учетом вопросов их практической реализации с требуемой точностью. Данная задача требует решения целого ряда частных проблем: выбора варианта построения устройства, элементов схемной реализации, разработки схемы и программного обеспечения и т.д. Решение поставленных задач требует знания современной элементной базы, схемных решений и методов программирования.
Исходя из вышесказанного, в третьей главе работы для решения вопросов практической реализации алгоритмов формирования и обработки ФМн сигналов, робастных к мешающим факторам, необходимо решить следующие задачи:
1. Разработать на основе критерия максимума удельной энтропии алгоритмы синтеза ФМн сигналов, робастных к искажению отдельных символов.
2. Разработать алгоритмы многокритериального синтеза составных ФМн сигналы и устройств их обработки.
3. Синтезировать форму модулирующей функции ФМн сигналов, обеспечивающую при минимальных потерях на обработку фиксированную скорость спада уровня внеполосных излучений.
4. Регуляризировать решение задачи синтеза ВФ устойчивого к неточности задания коэффициентов.
5. Рассмотреть вопросы программно-аппаратной реализации устройства формирования и обработки ФМн сигналов.
Как было отмечено выше, наиболее часто в качестве основного и единственного критерия синтеза ФМн сигналов выступает критерий минимума УБВ отклика СФ, а также критерий минимума среднеквадратического или среднестепенного отклонения формы отклика СФ от некоторой идеализированной формы. Использование данных критериев позволило получить ФМн сигналы с низкими значениями УБВ, в том числе и минимаксные сигналы.
Однако такие важнейшие характеристики РТС, как помехоустойчивость устройств обработки при действии мешающих факторов, потери в трактах формирования и обработки и т.д. в значительной степени определяется спектральными характеристиками используемых ФМн сигналов. Как было показано выше, для достижения робастности устройств обработки к действию мешающих факторов необходимо синтезировать сигналы с наиболее равномерной СПМ в рамках заданных ограничений. Для этой цели удобно использовать информационный критерий максимума удельной энтропии
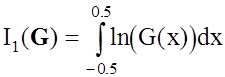, (3.1)
где G(x) - СПМ синтезируемого сигнала.
Дополнительным обоснованием использования спектральных критериев при синтезе ФМн сигналов может служить тот факт, что величина боковых выбросов отклика СФ связана с неравномерностью формы СПМ [88, 92], т.е. сигналы, имеющие минимальные значения среднеквадратического отклонения УБВ и одновременно малый их уровень, обладают и гладкими спектрами. Следовательно, для получения минимального УБВ отклика СФ необходимо синтезировать сигналы с минимально неравномерной, гладкой СПМ, что также можно сделать с помощью критерия максимума удельной энтропии сигнала, т.к. данный критерий гарантирует максимальную близость СПМ к равномерной в рамках заданных ограничений.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.