Тогда можно показать [73], что для заданной модели сигнала с параметрами mU и sU2вероятность правильного обнаружения рассчитывается по формуле:
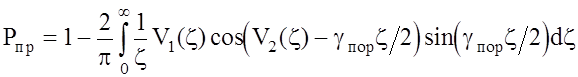 , (2.17)
, (2.17)
а ложной тревоги:
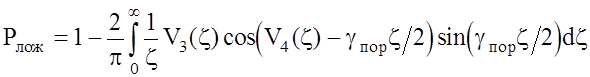 , (2.18)
, (2.18)
где вспомогательные коэффициенты V1(z),…,V4(z) имеют вид
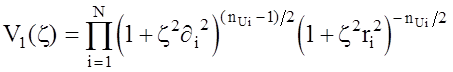 , (2.19)
, (2.19)
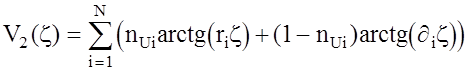 , (2.20)
, (2.20)
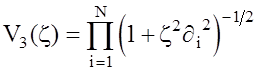 , (2.21)
, (2.21)
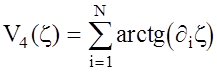 . (2.22)
. (2.22)
Из выражений (2.17) - (2.22) следует, что временные флуктуации ЭЦО через параметры распределения амплитуд nUi отдельных импульсов принимаемого сигнала влияют на вид характеристик обнаружения. При этом характеристика обнаружения пространственно распределенного объекта зависит от СПМ зондирующего сигнала.
Характеристика обнаружения в случае отсутствия временных флуктуаций, рассчитанная по приведенным формулам при вероятности ложной тревоги Pлож = 10-3, показана на рис. 2.2, кривая 1. Для расчетов использовался гипотетический пространственно распределенный объект из пяти светящихся точек [73]. Влияние формы СПМ сигнала на характеристики обнаружения пространственно распределенного объекта анализировалось при среднеквадратическом отклонении временных флуктуаций ЭЦО, равном 1/4 элемента разрешения для сигналов с СПМ вида cos4(px) (УБВ -47 дБ) и cos(px) (УБВ -23 дБ), которые приведены на рис. 2.2 (кривые 2 и 3 соответственно). Как следует из анализа этих кривых, временные флюктуации ЭЦО могут приводить к потерям в отношении сигнал-шум на 7 ‑ 15 дБ.
Для минимизации влияния временных флюктуаций ЭЦО необходимо синтезировать СПМ сигнала, имеющего АКФ с максимально плоской вершиной (в идеале прямоугольной) и низким УБВ. Искомую СПМ G(x) будем описывать M-мерным вектором
G = {G(x1),G(x2),...,G(xM)},
координатами которого являются отсчеты СПМ G(x) на регулярной
сетке 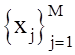 , где
интервал (x1, xM)
соответствует области определения G(x).
, где
интервал (x1, xM)
соответствует области определения G(x).
Согласно (2.17), некоторому M‑мерному вектору G ставится в соответствии вероятность правильного обнаружения Pпр. Таким образом, на некоторой совокупности M-мерных векторов G определен нелинейный оператор:
Ñ(G, r) = Pпр(r). (2.23)
Пусть ÂM - M-мерное эвклидово векторное пространство, ÀM - замкнутая область в нем, определяемая условием:
ÀM = {G Î ÂM : G(xi) ³ 0, i = 1, 2, ..., M}. (2.24)
Пусть Pпр0(r) - заданная на отрезке (rI, rII) функция из пространства L2. В этом случае под точностью решения понимается:
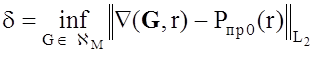 . (2.25)
. (2.25)
Таким образом, задача синтеза будет состоять в определении такого вектора G, при котором величина d будет минимальной. Согласно [28], элемент G, минимизирующий при заданной Pпр0(r) функционал (2.25), являться квазирешением.
Если ÀM - компакт, то квазирешение существует для любой Pпр0(r) из L2. Если условие единственности решения уравнения (2.23) не выполнено [28], то квазирешение образует некоторое множество À*M элементов компакта ÀM. В этом случае имеет место непрерывная зависимость множества квазирешений À*M от Pпр0(r) в смысле непрерывности многозначных отображений [28].
В общем случае множество ÀM слишком широкое. Кроме того, при неточно заданной правой части Pпр0(r) = Pпрd(r) уравнения (2.23) такой, что
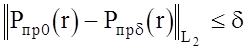 (2.26)
(2.26)
произвольный элемент Gd из ÀM, удовлетворяющий (2.25), не будет, вообще говоря, устойчивым относительно малых изменений Pпрd(r).
Таким образом, поставленная задача должна рассматриваться как некорректная, поэтому для получения устойчивых решений используется метод регуляризации, основанный на идее стабилизации минимума уклонения значений Ñ(G, r) от заданной правой части Pпр0(r) при помощи стабилизатора W[G], определенного на некоторой части пространства решений ÀM. При этом необходимо решить задачу минимизации сглаживающего функционала [55]:
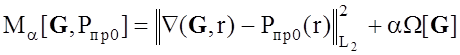 . (2.27)
. (2.27)
Определение параметра регуляризации a осуществляется в соответствии с принципом невязки:
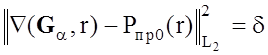 , (2.28)
, (2.28)
где d - величина, характеризующая точность задания
правой части уравнения (2.23). Необходимо отметить, что в случае нелинейного
оператора Ñ не гарантируется [28] строго
монотонной и непрерывной зависимости невязки 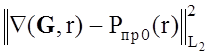 от
параметра a. Однако если воспользоваться свойством выпуклости
оператора Ñ в выражении (2.23), т.е. считать, что для любых G1
и G2
выполняется неравенство:
от
параметра a. Однако если воспользоваться свойством выпуклости
оператора Ñ в выражении (2.23), т.е. считать, что для любых G1
и G2
выполняется неравенство:
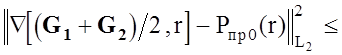
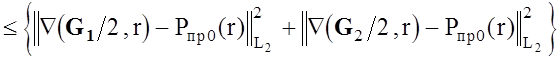
то, согласно [55], параметр a можно определять в соответствии с (2.28).
Стабилизирующий функционал W[G] в (2.27) обеспечивает функцию сужения пространства решений в соответствии с заранее задаваемыми критериями, входящими в постановку задачи.
В рассматриваемом случае, как было отмечено выше, физическая природа отражений сигнала от пространственно распределенного объекта приводит к появлению амплитудных модуляционных искажений отраженного сигнала. Для минимизации влияния данных искажений требуется, как было показано в разделе 1.4, использовать сигналы с минимальным коэффициентом частотно-временной связи.
Поэтому при синтезе сигналов для обнаружения пространственно распределенных объектов вид стабилизирующего функционала целесообразно задавать выражением:
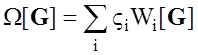 (2.29)
(2.29)
где Vi, i = 6 ¸ 8 - весовые множители; Wi[G] - функционалы, определяющие выбранные показатели качества. Выбор данных показателей качества обоснован в разделе 1.4 требованием минимизации влияния модуляционных искажений амплитуды сигнала. Функционал W6[G] ограничивает величину коэффициента частотно временной связи
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.