Наконец, наиболее универсальным и гибким являются специальные методы ограничения занимаемой полосы частот [115], основанные на изменении закона модуляции отдельных символов сигнала. Как показано в [37], все методы ограничения полосы делятся на амплитудные, фазовые и амплитудно-фазовые. В амплитудных методах для ограничения полосы используют уменьшение амплитуды огибающей в момент перескока фазы колебаний. При фазовых методах обеспечивается постоянство амплитуды, а уровень внеполосных излучений снижается за счет выбора определенной фазовой структуры символов сигнала. При использовании амплитудно-фазовых методов результирующее колебание имеет как амплитудные, так и фазовые изменения. Таким образом, при всех методах ограничения полосы применяется дополнительная амплитудная и/или фазовая модуляция символов исходного ФМн сигнала.
Применение указанных методов ограничения полосы в системах связи приводит к энергетическим потерям по сравнению с системами, где используются классические ФМн сигналы. Величина потерь зависит как от формы модулирующей функции, так и от применяемого метода ограничения полосы частот.
На практике [115] при выборе модулирующих функций используют либо критерий максимальной концентрации энергии в заданной полосе частот, либо критерий обеспечения максимальной скорости спада уровня внеполосных излучений. Как показано в [37], по первому критерию к оптимальной модулирующей функции близка функция вида cos(x), а по второму - cos2(x). Этим объясняется широкое практическое применение модулирующих функций данных видов [115]. Однако оптимальность по одному из критериев приводит к серьезному проигрышу по другому критерию, а также высокому уровню энергетических потерь [37].
С точки зрения помехоустойчивости сигналов с дополнительной модуляцией отдельных символов необходимо минимизировать как требуемую полосу частот, так и энергетические потери при обработке. Таким образом, задачу синтеза модулирующей функции символов ФМн сигналов, минимизирующей энергетические потери при обработке и требуемую полосу частот, необходимо рассматривать как многокритериальную
Представим ФМн сигналы в виде последовательности N импульсов, сформированных с учетом амплитудных и фазовых методов ограничения полосы частот
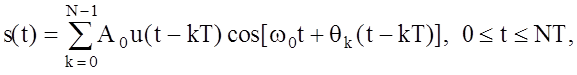(3.21)
где w0 - несущая частота, A0 - амплитуда сигналов, qk(t) = dkq(t), dk = ±1, u(t), q(t) - огибающая и закон изменения фазы отдельного символа длительностью T. В дальнейшем будем оперировать абстрактной модулирующей функцией m(t), которая может быть использована как при амплитудных так и при фазовых методах ограничения полосы. Äëÿ формализации задачи многокритериального синтеза модулирующей функции m(t), рассмотрим выражение для энергетических потерь при амплитудном методе ограничения полосы частот, возникающих при обработке модулированных ФМн сигналов по сравнению с классическими
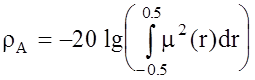(3.22)
где r = t/T, m(0) = 1. Выражение (3.22) соответствует случаю приема независимых ФМн сигналов при когерентной обработке и предположении о постоянной пиковой мощности передатчика [37]. Нетрудно заметить, что при m(r) ® rect(r), ½r½ < 0.5 энергетические потери отсутствуют. Тогда критерием качества, показывающим степень приближения формы моделирующей функции m(r) к прямоугольной, может служить функционал вида
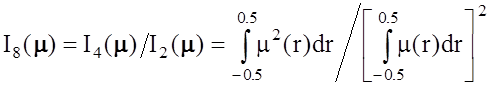. (3.23)
Из анализа выражения (3.23) следует, что минимизация функционала (3.23) приводит к минимуму энергетических потерь при m(r) = rect(r), ½r½ < 0.5.
Другим критерием качества синтезируемой функции m(r), позволяющим минимизировать требуемую полосу частот, является функционал, позволяющий оценить эффективную полосу частот 2b, занимаемую модулирующей функцией m (r)
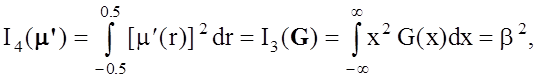(3.24)
где G(x) - спектральная плотность мощности функции модуляции m(r).
Кроме перечисленных выше критериев качества, целесообразно использовать показатель скорости убывания уровня внеполосных излучений. Для этой цели, введем в качестве дополнительного условия при синтезе модулирующей функции m(r) функционал вида
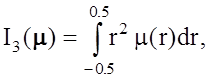(3.25)
позволяющий, как будет показано ниже, эффективно влиять на скорость убывания уровня внеполосных излучений.
При введенных критериях качества задача многокритериального синтеза модулирующей функции m(r) может быть поставлена как задача минимизации векторного показателя качества
I(m) = {I4(m'), I8(m)}, (3.26)
при наличии ограничивающего условия (3.25), здесь функционалы I4(m') и I8(m) описываются соответственно выражениями (3.23), (3.24).
Для отыскания множества нехудших функций воспользуемся безусловным критерием предпочтения [25], в рамках которого все показатели качества, кроме одного, переводятся в разряд ограничений. В силу интегрального характера функционалов (3.23), (3.24) и условия (3.25), рассматриваемая задача относится к изопериметрическим задачам вариационного исчисления. Для данного типа задач характерен принцип взаимности [44], исходя из которого рабочие поверхности, получаемые при минимизации отдельных показателей качества, совпадают.
Следовательно, рассматриваемая задача эквивалентна задаче минимизации следующего вспомогательного функционала [44]
I(m) = I4(m) + l31I4(m') + l32I3(m) + l33I2(m), (3.27)
где l31 , l32 , l33 - множители Лагранжа. Стационарные точки функционала (3.26) находятся как решения уравнения Эйлера-Лагранжа
(3.28)
Тогда решение дифференциального уравнения (3.28) может быть получено в виде [116]
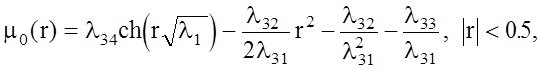(3.29)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.