Основные понятия моделирования. Виды моделирования. Этапы создания модели. Задачи математического программирования

            Основные  понятия  моделирования

 Введение. Виды  моделирования.

Моделирование  представляет  собой  процесс  замещения  объекта  исследования  его  моделью  и  проведение  исследований  на  модели  с  целью  получения  необходимой  информации  об  объекте.

Модель – это  физический или  абстрактный  образ  моделированного  объекта,  позволяющий  адекватно  (с   приемлемой  точностью)  отображать  интересующие  нас  физические  свойства  и  характеристики  объекта.

Целью  моделирования  является:

1.  Выделение  наиболее  существенных  факторов,  которые  формируют  основные  характеристики  объекта.

2.  Пробуя  различные  варианты  управления,  мы  подбираем  оптимальный  алгоритм  управления  на  модели  объекта.

3.  Имея  модель,  мы  сможем  предсказать  значения  выходных  характеристик  реального  объекта  для  заданных  входных  объектов.

Рассмотрим  два  основных  вида  моделирования:

1.  Материальное

2.  Идеальное

При  материальном  моделировании  мы  воспроизводим  все  основные  физические,  функциональные,  динамические  и  геометрические  характеристики  изучаемого  объекта.

Различают  физическое  и  аналоговое  моделирование.

При  физическом  моделировании  реальному  объекту  сопоставляется  его  копия.  Исследования  проводятся  на  этой  копии,  а  изучаемые  свойства  переносятся  на  изучаемый  объект  на  основании  теории  подобия.

Аналоговое  моделирование  основано  на  функциональной  аналогии  процессов  и  явлений,  имеющих  различную  природу,  но  описанных  одними  и  теми  же  математическими  уравнениями  (уравнения  колебания).

Идеальное  моделирование  носит  теоретический  характер.  В данном  случае  модель  является  не  идеальной,  а  материальной.

Различают  две  разновидности:

Интуитивное  моделирование 

Знаковое   (знак,  символ)

   Интуитивное  моделирование  основывается  на  интуитивном  представлении  об  объекте  исследования.

Знаковое  используют  в  качестве  модели  знаковое  соответствие  некоторого  вида  схемы,  чертежа,  графики,  формулы. В этом  разряде  важнейшим  видом  является  математическое  моделирование,  оно  замещает  реальный  объект  его  математическим  образом  (формула).  Процесс  формирования  математической  модели  и  ее  использование  для  анализа  называется  математическим  моделированием.  В  конструкторской  практике  под  математическим  моделированием  обычно  понимается  процесс  построения  математической  модели,  а  проведение  исследования  на  модели  называют  вычислительным  экспериментом. 

Системный  подход  к  математическому  моделированию.

Создание  модели – сложный  процесс,  который  в  ряде  случаев  может  быть  длительным  во  времени,  поэтому  используют  системный  подход.

Исследуемый  объект  с  одной  стороны  рассматривается  как  элемент,  реализующий  самостоятельную  задачу  и  связанный  материальными,  энергетическими  и  информационными  связями  с  другими  элементами  системы,  а  с  другой  стороны  как  самостоятельная  сложная  система,  которая  может  быть  предложена  как  совокупность  элементарных  звеньев  (процессов).

 ¾®                             ¾® 

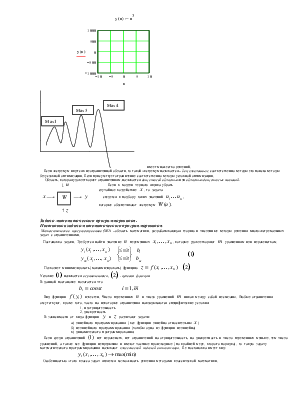
Связи,  которые  воздействуют  на  систему,  называют  входными.  Связи,  при  помощи  которых  система  воздействует  на  окружающую  среду,  называют  входными.F- целевая функция. 

     Если  известны  связи  между  элементами,  то мы говорим о структуре системы.                                                                                                                                                                                                 Некоторый  элемент  системы  может  состоять  из  известных  элементов,  то  тогда  говорят  о  подсистемах.       

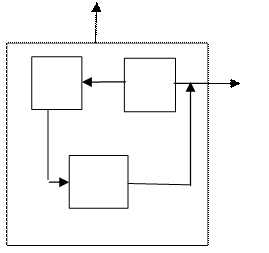Процесс  определения  внутреннего  состава  системы  называется  декомпозицией.                                               

Классификация  системы

1.  По  характеру  связи    и  :

а) дискретные  (если    и    принимают  конкретные  значения)

б) непрерывные

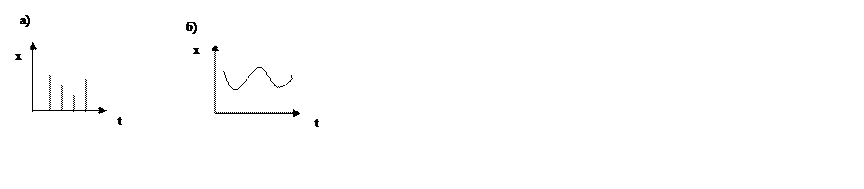
в) линейные  (, где   – линейный  оператор). Зная  , мы  можем  однозначно  вычислить  . г) нелинейные  (присутствует  некоторое  случайное  воздействие  ).  Если  случайное  воздействие    отсутствует,  а  связь  между    и    является  однозначной,  система  называется  детерминированной,  в  противном  случае – недетерминированной.  Недетерминированная  система  описывается:

1.  системой  уравнений

2.  матричными  операциями

3.  графиками,  векторами

В  недетерминированных  (стохастических)  значения  y  можно  представить  только  с  некоторой  вероятностью.

  Требования  к  математическим  моделям

1.  адекватность;

2.  экономичность;

3.  универсальность.