3. Оцениваем адекватность модели реальным данным.
4. Отливаем незначимые коэффициенты регрессии.
Решение в MathCAD (пример)
1. Проведение эксперимента и заполнение таблицы
Вводим в MCAD вектора (либо в виде матрицы, либо в виде векторов)
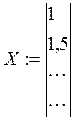
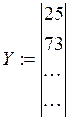
2. Вид зависимости. Строим график Y(X) . Вектор Х должен быть упорядочен по возрастанию.
3. Рассчитывается коэффициент корреляции
![]()
Если значения в векторах сильно связаны, то коэффициент корреляции = 1.
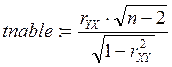 , n:=length(X), где n –
число элементов в векторе.
, n:=length(X), где n –
число элементов в векторе.
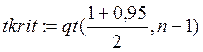
|tnable| > tkrit, то рассчитываем и анализируем коэффициент детерминации.
![]() - если = 0,8 , то в 80%
случаев объясняется наличием зависимости между Y и Х и только 20%
случайным воздействиями.
- если = 0,8 , то в 80%
случаев объясняется наличием зависимости между Y и Х и только 20%
случайным воздействиями.
4. Подбор моделей
![]() > 0,9 – линейная модель
> 0,9 – линейная модель
> 0,8 – квадратичная модель
Вxy = > 0,5 – полином (старшая степень больше 2-х)
< 0,5 – нет смысла строить модель
Y(X) = kX+b - линейная модель
Если 0,83, то лучше выбрать квадратичную модель ![]()
Предположим, мы решили, что модель квадратичная,
тогда нам необходимо рассчитать коэффициенты ![]() .
.
К:=0,1,…,n-1
Ек:=1
ХХ<0>:=E
![]() XX<1>:=X
XX<1>:=X
XX<2>:=X*X – поэлементное умножение векторов
F:= ![]() - Матрица F
- Матрица F
B:= ![]() -
Матрица В
-
Матрица В
Проверка |F|![]() - определитель |F|
- определитель |F|![]() -если не нуль, то вычисляем:
-если не нуль, то вычисляем:![]()
В результате получим квадратичную зависимость : ![]()
2). Оценка адекватности
AA:=Var(Y)n , Var(Y) – дисперсия вектора Y
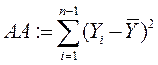 , где
, где ![]() - среднее значение, АА –
суммарное отклонение экспериментальных точек от их среднего.
- среднее значение, АА –
суммарное отклонение экспериментальных точек от их среднего.
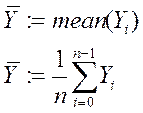
Вычисляем вектор прогнозируемых моделью значений в точках Х1,…,Хn.
W:=XX*A
Wi:=Y(Xi)
3). Вычисляем суммарную ошибку отклонения прогнозируемых значений от экспериментальных:
![]()
4). Определяем число параметров модели
Nr = 2 – линейная модель
Nr = 3 – квадратичная модель
Nr = m+1, если полином n-ой степени.
5).
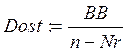 Вычисляем остаточную дисперсию
Вычисляем остаточную дисперсию
6).
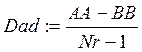 Вычисляем дисперсию адекватности
Вычисляем дисперсию адекватности
7). Проверяем гипотезу об адекватности:
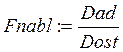
Fkrit:=qF(1-![]() ,
Nr, n-Nr) ,
,
Nr, n-Nr) , ![]() :=0,05 – уровень значимости для технологических систем.
:=0,05 – уровень значимости для технологических систем.
Если Fnable > Fkrit , то модель адекватна и ее можно использовать в расчетах.
4.Отсев незначащих коэффициентов регрессии
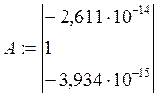
только 1 коэффициент имеет влияние, т.е. модель линейная.
Функция примет примерно следующий вид: ![]()
Примечание к одномерной модели
1. Формулы верны для любого вида функций
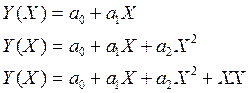
Вектор прогнозируемых значений рассчитывается по формуле W=XX*A
2. В расчете оценки адекватности используется только одна характеристика. Количество параметров модели.
Модель регрессионного анализа для многомерного случая
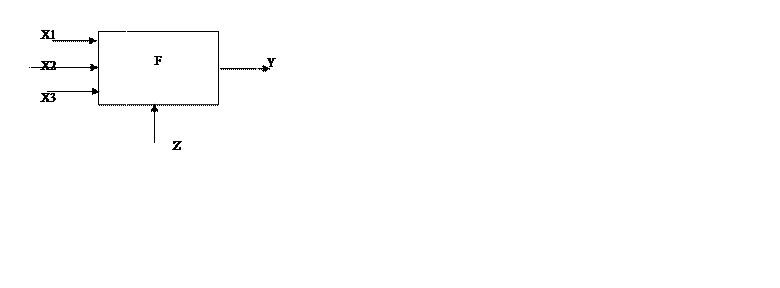 При исследованиях мы
ограничимся только линейной зависимостью
При исследованиях мы
ограничимся только линейной зависимостью
Y(X1,X2,…,Xm)=![]()
Схемы решения аналогично одномерного случая, за исключением:
1. графики не строят
2. коэффициент детерминации не рассчитывают.
Последовательность:
1. Проводится эксперимент в n точках. В каждой точке измеряют m входных значений и одно выходное (Х1, Х2,…,Хm и Y) . в результате получают таблицу:
|
Х1 |
|
|
|
|
|
|
||
|
Xm |
|
|
|
|
Y |
Y1 |
Yn |
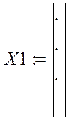
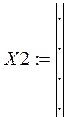
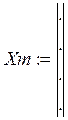
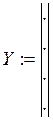 длина
всех векторов n
длина
всех векторов n
2. Рассчитываем коэффициенты уравнения линейной регрессии:
k:=0, 1, … , n-1
Ek:=1 единичный вектор
XX<0>:=EXX<1>:=X1 XX<2>:=X2 … … XX<m>:=Xm
F:= ![]()
B:=![]()
Далее проверяем определитель матрицы |F| , если он равен 0, то вычисления прекращаем. Если не равен 0, то вектор коэффициентов находим следующим выражением:
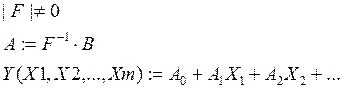
3. Проверяем адекватность (те же формулы, что и для одномерной модели).
W:=XX*A
AA:=N*Var(Y)
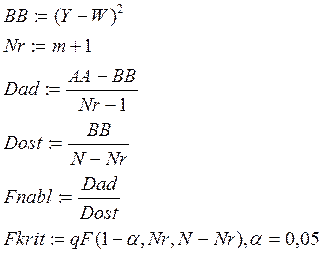
Если Fnabl > Fkrit, то модель адекватна, и ее можно использовать в расчетах.
4. Отсев несущественных факторов многомерной модели (оценка значимости коэффициентов регрессии) :
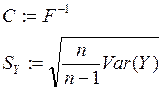
5. Находим среднеквадратичное для каждого коэффициента:
![]()
Рассчитываем наблюдаемый критерий:
tnabl:=![]()
![]()
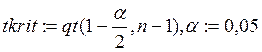
Если |tnabl| > tkrit , то коэффициент ![]() значимо влияет на выходной фактор Y; в
противном случае – незначимо.
значимо влияет на выходной фактор Y; в
противном случае – незначимо.
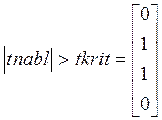 , т. е. 0 – незначимо,
1 – значимо.
, т. е. 0 – незначимо,
1 – значимо.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.