Основные понятия моделирования. Виды моделирования. Этапы создания модели. Задачи математического программирования, страница 12

Процентное  содержание меди (Cu) в сплаве	1%	2%	3%
	A1	A2	A3

Проведя  однофакторный  анализ, получим  ответ  на  вопрос: значимо  или  незначимо  влияние  содержания  меди  от  1  до  трех  процентов  на  твердость  сплава.

Пример 2

В  цехе  имеется  М  однотипных автоматных  линий,  производящих  одинаковую  продукцию. Для  каждой  линии  делается  выборка  из  n  элементов.

Однофакторный  анализ  в  этом  случае  дает  ответ  на  вопрос  значимо  или  незначимо  влияние  номера  линии  на  ее  производительность.  В  роли  фактора  А  выступает  номер  линии, в  роли  случайной  величины – производительность.

Пример 3

Необходимо  провести  совместный  анализ  точности m  одинаковых  приборов. Для  этого  каждым  прибором  выполняется  n  измерений  в  одинаковых  условиях. Нужно  узнать  значимо  или  незначимо  отличаются  погрешности  приборов. В  роли фактора  А выступает  номер  прибора, в  роли  случайной  величины  x – величина  погрешности  прибора. Для  однофакторного  анализа  выполняется  n  измерений  каждым  прибором.

Схема  применения  однофакторного  анализа.

Для  проверки  гипотезы  о  значении  влияния  некоторого  фактора  А  на  изучаемую  величину  x  задается  некоторая  величина  к,  которую  называют  критерием, который  подчиняется  определенным  известным  законам  распределения. Задается  уровень  значимости  и  решается  обратная  задача  статистического  моделирования  для  уравнения:

,  где - уровень значимости, w – критическая область.

Все  сводится  к  определению  того,  попадает  или  нет  наблюдаемое  значение  критерия  к  в  критическую  область. Для модели  однофакторного  анализа  критерий  к  имеет  распределение  Фишера,  и  уравнение  имеет  вид

Если  , то принимается  гипотеза  .

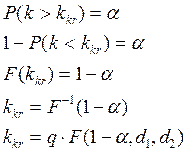
где   - степени  распределения ().

Далее  нужно  принять  решение.

Если , значит,  применяется  гипотеза . Если , то гипотеза  .

Выполнение  однофакторного  анализа  в  среде  MathCAD.

1. Задается  матрица  выборки (m*n, где  n – количество  опытов  на  каждом  уровне  фактора, m- количество  уровней  фактора).

2. Рассчитывается  выборочное  среднее  по  формуле

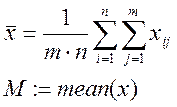
3. Рассчитываются  выборочные  средние  дисперсии  по  каждому  уровню  фактора      

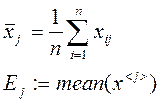
Затем  вычисляются  групповые  дисперсии

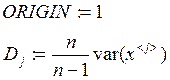
4. Рассчитывается  межгрупповая  дисперсия, описывающая  влияние  исследуемого  фактора.

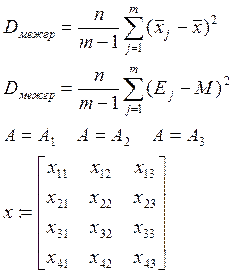
Отличие  столбиков  матрицы  x  обусловлено  влиянием  исследуемого  фактора

Вычисляется  остаточная  дисперсия.

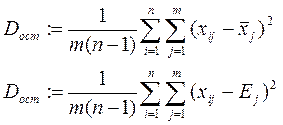
Остаточная  дисперсия  описывает  влияние  всех  остальных  факторов  кроме  фактора  А.

5. Вычисляется  значение  критерия

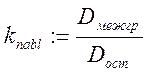
 имеет  распределение  Фишера.

6. Выполняется  проверка  однородности  групповых  дисперсий  с  помощью  критерия  Фишера

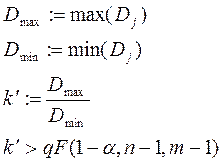
Если  оказывается,  что  , то  величины  неоднородны, и  схему  однофакторного  анализа  применять  нельзя.

Основные понятия моделей: корреляционный и регрессионный

1. Факторы  x1, x2→ влияют на y. В математическом анализе зависимость между двумя величинами  характеризуется функцией

- функциональная зависимость.

Для случайных величин X, Y в общем случае установить функциональную зависимость невозможно.

  Пример

Если взять большие выборки, то нельзя установить рост человека.

Между СВ может существовать зависимость особого рода, при которой с изменением одной величины изменяется статистическое распределение другой, такая связь называется стохастическая. Изменение СВ Y соответствующее изменению величины X при этом разбиваются на две компоненты:

1. стохастическая, которая связана с распределением одной величины в зависимости от другой

2. случайная (все кроме стохастической)

В случае, когда стохастическая компонента отсутствует величины X и Y независимы. Соотношение между стохастической и случайной компонентой определяет силу связи между СВ X и Y. Эту связь называют корреляционной. Одним из показателей стохастической связи является коэффициент корреляции. Из теории вероятности известно, что дисперсия суммы двух независимых СВ X и Y равна сумме их дисперсий.