Основные понятия моделирования. Виды моделирования. Этапы создания модели. Задачи математического программирования, страница 14

(*), (**) – корреляционные уравнения или уравнения регрессии, а функции в правых частях f(x)  и  называются функциями регрессии.

Графики этих функций называются линией регрессии. Пользуясь приведенными выше таблицами, можно установить с помощью какой именно функции зависимость можно описать корреляционную связь между X и Y.

В связи с этим в теории корреляции решаются две основные задачи:

1. По данным корреляционной таблицы  1 нужно определить форму корреляционной связи, т. е. конкретный вид функций .

2. Дать оценку степени рассеяния значений Yоколо среднего значения Y(x) или разброса значений. Так как среднее значение представляет собой истинное значение наблюдаемой величины, то регрессия дают истинную зависимость  Y(x) лишенную всяких случайных влияний.

В общем случае задачи регрессионного анализа формируются так. По известной выборке, получаемой из опыта , найти уравнение регрессии и оценить допускаемую при этом ошибку.

Уравнение регрессии – это математическая модель, справедливость которой мы предполагаем. Модели могут быть разного вида, например, линейная модель

, квадратичная модель . Как правило, задачи регрессионного анализа сводятся к отысканию коэффициентов уравнения регрессии. Выбор уравнения регрессии является важной частью решения задачи. Чаще всего этот выбор делается на основе предыдущих знаний об исследуемой модели. Для двумерной СВ выбор вида модели можно сделать по расположению точек в плоскости (x, y). 

Определив общий вид функции регрессии, получим класс сравниваемых функций  

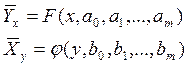
где  - описывает значение y,

 - значение x.

Примером такого класса функций может быть множество многочленов в степени n, тогда в качестве коэффициентов функции регрессии выступают

Чтобы выбрать среди множества функций такого вида наилучшую нужно найти ее коэффициенты и определить ошибку аппроксимации. Оценить погрешность аппроксимации можно, используя метод наименьших квадратов. Этот метод позволяет определить конкретный вид коэффициентов в уравнении регрессии при минимальной квадратичной ошибке. Если задан некоторый класс функции вида

, которая имеет m+1 параметров. Наилучшее уравнение для которой

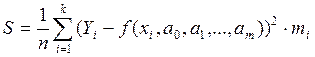, где  n – количество опытов

- количество опытов, при которых измерялась пара значений .

Уравнение возводим в квадрат для того, чтобы исключить влияние знака абсолютной ошибки.

Величину m+1 равную числу параметров уравнения регрессии называют числом связей накладываемых функцией регрессии на наблюдаемые данные, т. е. число связей равно количеству параметров, по которым нужно найти min функции S.

Таким образом, с помощью метода наименьших квадратов отыскиваются коэффициенты уравнения регрессии на основе минимизации суммарной среднеквадратичной ошибки.

Общие меры рассеивания

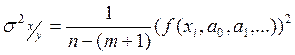
При выборе уравнения регрессии, стремятся к минимально необходимому количеству параметров.  Обычно в качестве функции регрессии выбирают линейную регрессию, значение находят по аппроксимации. Если ошибка больше чем нам задана, то выбирают следующую функцию (квадратичную) и снова делают проверку на ошибки и т. д.

Различают регрессию простую и множественную. Для двумерной СВ регрессия простая, при большей размерности СВ регрессия множественная (3 и более)

Пример  Простая регрессия – это регрессия между номером остановки и количеством пассажиров, множественная – количество пассажиров, номер остановок, день недели.

Метод наименьших квадратов.

Линейная регрессия

Пусть поле корреляции имеет вид линейной функции ,

Тогда ошибка от замены опытных данных точками графика функции регрессии в точке к:.

Сумма квадратов этих ошибок по всем точкам  определяют суммарную ошибку                          

Суммарная ошибка будет минимальной при таких значениях коэффициентов  и , когда функция F имеет глобальный минимум. Для нахождения минимума этой функции приравнять ее частную производную к нулю.

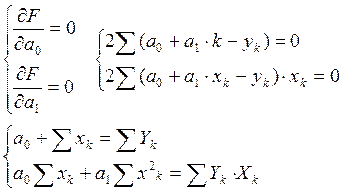
Полученную систему можно представить в виде матричного уравнения

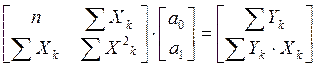
Введем обозначение

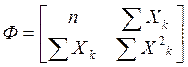
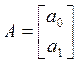
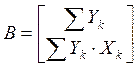                                , тогда система уравнений примет следующий вид

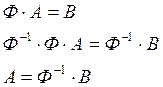
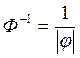 , если  .