Если при обработке данных Ф=0, то такой метод расчета использовать нельзя, нужно выполнить дополнительные опыты.
В пакете MathCAD есть встроенные функции для нахождения коэффициентов линейной регрессии.
, где
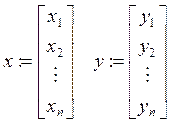
Нахождение коэффициентов регрессии
Линейная регрессия
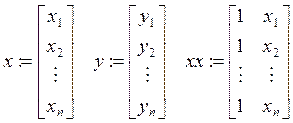
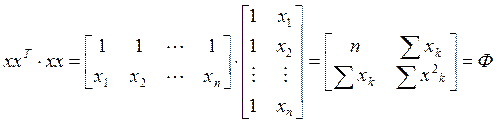
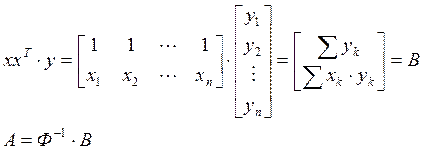
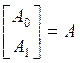- вектор коэффициентов линейной регрессии.
Преимущество состоит в том, что не нужно брать производные, все сводиться к матричным операциям, которые легко выполняются с помощью математических пакетов, в частности пакета MathCAD.
Матрицы имеют специальное назначение. Ф- информационная матрица (матрица Фишера), xx- матрица исходных данных.
Пример расчета в пакете MathCAD.
1. На основе корреляционной таблицы заполненной по опытным данным строим векторы исходных данных.
|
x\y |
9 |
10 |
11 |
12 |
|
4 |
2 |
1 |
0 |
0 |
|
5 |
0 |
2 |
0 |
0 |
|
6 |
0 |
1 |
1 |
1 |
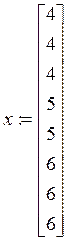
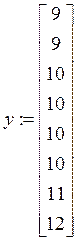
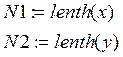
2. Строим матрицу исходных данных
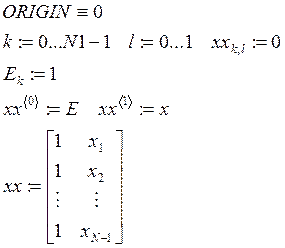
3. Строим информационную матрицу
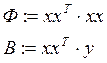
4. Находим значение коэффициентов регрессии
- свободный член
- тангенс угла наклона
5. Задаем функции, строим графики
Ошибка такого расчета может быть определена методом остаточных сумм.
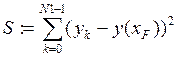
Нелинейная регрессия
Пусть зависимость между СВ x и y не является линейной. Предположим, что экспериментальные данные хорошо описываются линейной функцией
.
Применим метод наименьших квадратов и матричный метод.
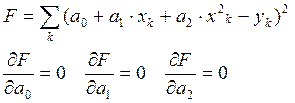
Проще использовать матричный метод. Порядок действий практически такой же, как и при вычислении линейной регрессии.
1.
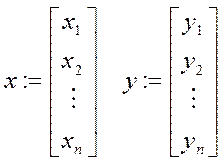
2.
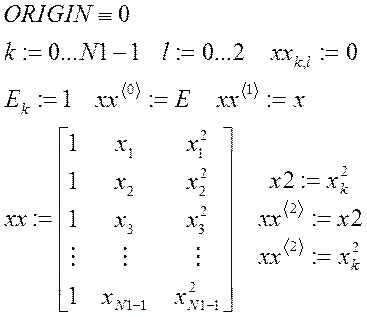
3.
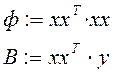
4.
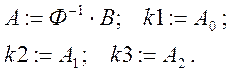
5.
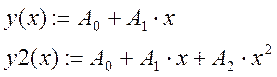
Если степень полинома регрессии больше двух, то матрица исходных данных изменяется следующим образом
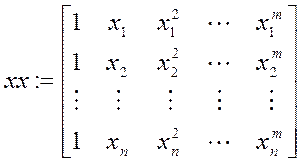
Данная схема легко реализуется в пакете MathCAD.
2.
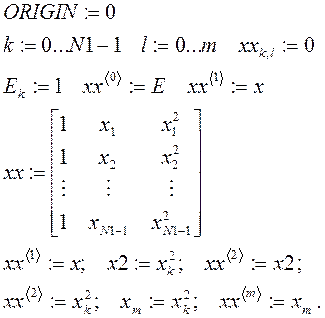
В случае,
если функция регрессии задается в линейной комбинации заданных функций, то 
.
Применяется матричный метод
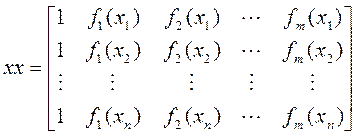, (N1-1).
Для вычисления таких значений удобно использовать операцию
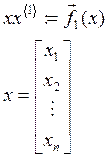
MathCAD позволяет поэлементно выполнять различные операции.
Линеаризация функции регрессии
Выше рассмотренные функции регрессии линейные по коэффициентам регрессии. Часто нужно находить коэффициенты нелинейных функций регрессии
В этом случае задача сводиться к линейной по коэффициентам линеаризации. Для этого прологарифмируем правую и левую часть
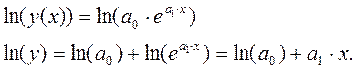
После логарифмирования мы получаем модель линейную по коэффициентам.
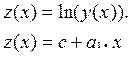
Функция ошибок для такой модели:
Z(Xk) теоретическая зависимость линейной регрессии
Yk(опыт).
Формула для А точно такая же.
3). 
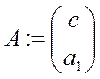
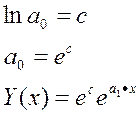
Данная модель относится к классу мультипликативных моделей.
Расчёт их параметров сводится к расчёту многих моделей путем линеаризации. Возможны более сложные модели, которые можно линеаризовать.
Операции линеаризации
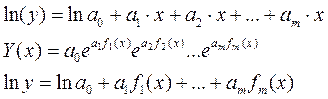
Для выбора из нескольких функций регрессии наилучшей проводится анализ качества приближения по остаточной функции
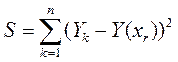
опыт
Если нужно суммирование ведется по всем опытным точкам.
По порядку величины, которая измерялась, т.е. ошибку, вносимую в одной точке, можно посчитать среднеквадратичную ошибку.
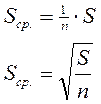
Из нескольких возможных функций регрессии выбирается та функция, где остаточная особа наименьшая, т.е. ошибка аппроксимации минимальная.
Встроенные функции МСAD
для регрессионного анализа
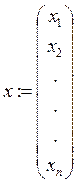
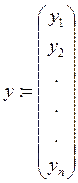
Исходные данные вектора x,y.
Как определить, имеет ли смысл строить регрессионные модели ?
Если 
то данные описываются
прямой линией.
Если 
то квадратная
зависимость.
Полиномиальная регрессия
Используется несколько встроенных функций:
regress
loess
interp
Функция regress используется, когда данные хорошо описываются одним полиномом:
Функция regress дает или позволяет использовать полином n-ого порядка. На практике степень полинома не выше 4.
regress(VX, VY,n) – возвращает вектор требуемой функции interp, чтобы найти полином порядка n, который наилучшим образом приближает данные из векторов VX и VY.
VX – есть вектор значений Х:
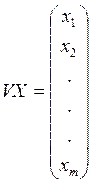
VY – есть вектор значений y:
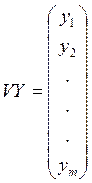
Вектора VX и VY описывают m опытных точек.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.