Основные понятия моделирования. Виды моделирования. Этапы создания модели. Задачи математического программирования, страница 11

Для  двухфакторного  дисперсионного  анализа  получим  выражение

 

, где   - суммарная  дисперсия

- составная  часть  дисперсии,  вызванная  фактором  А

- составная  часть  дисперсии,  вызванная  фактором  В

- часть  суммарной  дисперсии,  вызванная  общим  влиянием А  и  В

 -  часть  дисперсии,  вызванная  случайными  явно  не  учитываемыми  причинами,  которые  называют  случайной  или  остаточной  дисперсией.

При  проведении  дисперсионного  анализа  обычно  получают  выборку  необходимого  объема  из  генеральной  совокупности  значений  x.  На  основании  этой  выборки  находим  не  сами  дисперсии  случайной  величины  x,  а  только  выборочные  оценки  этой  дисперсии.  Изучение  переменных  факторов  по  их  дисперсиям  называется  дисперсионным  анализом. 

Рассмотрим  самый  простой  случай,  когда  дисперсия  наблюдений,  например  разброс  значений  прибора  известен  заранее – это  величина  ( - среднеквадратичное  отклонение ()).

Выборочная  исправленная  дисперсия, описывающая  разброс  значений   x определяется  в  этом  случае  по  формуле 

 

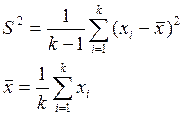
Величина  определяется  по  опытным  данным (по  величине  x).  Если  величины   и   отличаются  незначимо (), то  фактор  А  на x не влияет.  Если   (существенно  отличаются),  то  фактор  А  влияет  на  x.  

В  случае  несущественного  влияния  фактора  А  на x  мы  проводим  гипотезу  .     Гипотеза   состоит  в  том,  что  А  не  влияет  существенно  на  x -  нулевая гипотеза. Альтернативная  гипотеза   заключается  в  том,  что  фактор  А влияет  на x. Для  оценки доли  дисперсии  фактора  влияния  А  используется  то  обстоятельство, что дисперсия  суммы  двух  независимых  величин  равны  сумме  их  дисперсий   .  В  нашем  случае  складывается  эффект  случайности  имеющий  дисперсию  и  эффект  воздействия  фактора  А,  который  описывается  дисперсией    и  предполагается, что  эти  воздействия  независимы. Поэтому  общая  дисперсия  наблюдений  должна  быть  равна  сумме  этих  двух  величин.

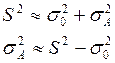
При  этом  оценивается  лишь  влияние  фактора  А  в  целом  на  величину  x , и  не  выясняются  количественные  соотношения. Сравнение  дисперсий   и   осуществляется  с  помощью  критерия  Фишера  по  формуле

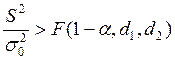, гдеF- распределение  Фишера

 - уровень  значимости

 - доверительная  вероятность

 - степени  свободы; ,  где  к – число изменений, .

Если  это  равенство  выполняется,  значит,  имеет  место  значимое  влияние  фактора  А на  величину  х, и  наоборот.

Однофакторный  дисперсионный  анализ (ОДА)

Рассмотрим  случай,  когда  значение  генеральной  дисперсии   неизвестно,  но  можно  предположить,  что  оно  одинаково  для  всех  изменений. Будем  считать,  что  за  время  всех  изменений  случайной  величины  x    , говорят, что  фактор  А  исследуется  на  m  уровнях. На  каждом  уровне  фактора  А  проводится  n  измерений (опытов) величины  x. По  результатам  измерения  заполняется  таблица.

№ опыта	Уровни  фактора  А
			…
1			…
2			…
…	…	…	…	…
n			…
Групповые средние			…

Средние  арифметические  значения  по  столбцам

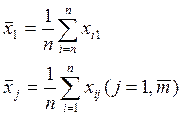
Величина   характеризует i – ое  значение  величины  x  для  j-го значения фактора  А (i- номер опыта,  j- номер  уровня).

Опираясь  на  статистические  данные  нужно  проверить  нулевую  гипотезу.

  

Нулевая  гипотеза  утверждает,  что  нулевые  средние  значения  x  на  каждом  значении  фактора  А  равны.  Следовательно,  фактор  А  не  влияет  значимо  на  x.

  Существует  значение  к, j, что   , где  .

Вывод:  фактор  А  значимо  влияет  на  величину  x.

Примеры  применения  ОДА.

Пример 1

1. Анализируя  влияние  содержания  некоторого  вещества (например,  медь)  на  определенные  свойства  сплава (например,  твердость), задается  несколько  процентных  уровней  содержания  данного  вещества  в  сплаве. Проводится n измерений  твердости  при  каждом  процентном  содержании.