Основные понятия моделирования. Виды моделирования. Этапы создания модели. Задачи математического программирования, страница 2

Модель  называется  адекватной,  если  отражает  исследуемые  свойства  реального  объекта  с  приемлемой  точностью.

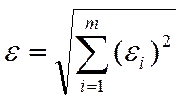
В  детерминированных  моделях  в  качестве  характерной  точности  берут  погрешности  модели  e  по  всей  совокупности  учитываемых  выходных  параметров.

                                          → 

→    

→ 

- число выходных  параметров;

- значение  выходного  параметра,  полученного  на  модели;

 - значение  выходного  параметра,  полученного  при испытании  реального объекта;

 погрешность  модели;

Стохастические  системы  в  стохастических  моделях  в  качестве  характеристики  адекватности  используется  вероятностная  оценка  надежности  принимаемого  решения.

   Экономичность  определяет  характеристики  стоимости:  стоимость  создания  модели,  объем  занимаемого  пространства,  время  цикла  обработки  одного  результата  и  т. д.  Как  правило,  выбирается  один  из  параметров  и  берется  на  контроль.

Универсальность  оценивается  широтой  класса  объектов,  для  которого  она  может  быть  применена.  

Этапы создания модели

1.  Определение  потребности,  анализ  проблем,  выделение  цели.

2.  Идентификация  системы.  Выделение  системы  из  окружающего  мира.

3.  Определение  состава  и  установление  связи  системы.

4.  Проверка  соотношения  целей  (оценка  адекватности,  экономичности).

5.  Оптимизация.  Она  заключается  в  упрощении  модели. 

Данные  этапы  выполняются   итерационно   с  откатом  назад.  Пока  не   будет  создана  система  (модель),  удовлетворяющая  заданным  целям.

Если  модель  создана  и  удовлетворяет  целям,  то  на  ней  проводят  вычислительные  эксперименты  с  целью  получения  новых  знаний  об  исследованном  объекте.

	F(x) система

 

 ¾®                            ¾® 

Оптимизация – подбор такого множества значений управляющих параметров , при которых критерий эффективности будет достигать своего экстремума.

Пакет MathCAD.

Символьные вычисления.   

1.  Символьный знак равенства ═

2.  Меню  Symbolic. 2 группы:

а) преобразование производится относительно выделенного выражения.

б) преобразование производится относительно одной переменной   

3.  Матричные операции.

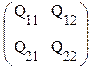
a)   нахождение определителя.  Последовательность  операций: меню  “символика”(symbolic)→ матрица (matrices) → определитель (determinant).

б) транспозиция.  Последовательность  операций:

меню  “символика”(symbolic)→ матрица (matrices) → транспозиция (transpose)

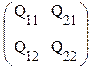
в) инвертирование. Последовательность  операций:

меню  “символика”(symbolic)→ матрица (matrices) → инвертирование (inverse)

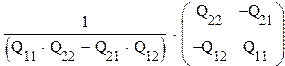
4.  Разложение в ряд.

   (разложение  производится  относительно  выделенной  переменной)

Поиск решений: системный подход.

	F(x) система

 

 – ?   ¾®                               ¾® 

    

Нам требуется при известной функции  и для заданных значений  найти соответствующее значение . Необходимо решить уравнение

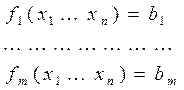
уравнений,

неизвестных.

При решении возможно 3 исхода:

1.   существует единственное решение (точное решение).

2.  существует множество решений (несколько, бесконечно много).

3.  решений не существует.

Наиболее хорошо изучены линейные системы, для  них  классической  математикой  разрешены  аналитические  методы  решения. Для нелинейных систем не существует общих методов решения. Для них используется поисковые методы, в которых решение ищется в соответствии с определением алгоритмом. Далее будем рассматривать 3 класса моделей: модели решения уравнений (систем уравнений); модели подбора приблизительных решений и модели поиска оптимальных решений.

Решение уравнений в системе

MathCAD.

Дано  уравнение  вида: ,  необходимо  найти  его  корни.

Поиск корней уравнения.

1.  Решение уравнений с помощью функции root позволяет  находить  уравнение  вида:

       

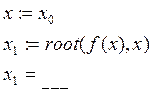
 Пример

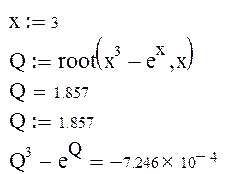
2.Решение уравнений с помощью функции Given.