Основные понятия моделирования. Виды моделирования. Этапы создания модели. Задачи математического программирования, страница 4

Если  среди  ограничений    нет  неравенств,  нет  ограничений  на  отрицательность,  на  дискретность  и  число  переменных  меньше, чем  число  уравнений,  а  также  все  функции  непрерывны  и  имеют  частные  производные  (по  крайней  мере,  второго  порядка),  то  такую  задачу  математического  программирования  называют  классической  задачей  оптимизации.  Ее  постановка  имеет  вид:

  

Особенностью  этого  класса  задач  является  возможность  решения  методами  классической  математики.

Задачи  линейного  программирования.

Задачами  линейного  программирования  заданными  в  произвольной  форме  называют  задачи,  в  которых  требуется  минимизировать (максимизировать)  функцию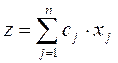                                                                                     

                                      

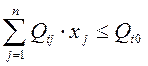
при  условиях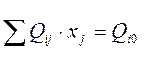                                                                              

                                                                                                           

- произвольная,                                                            

где   -  заданы.

Задачи  линейного  программирования  в  симметричной  форме

                                                    

                                                                                          

                                                                                                          

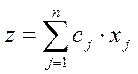
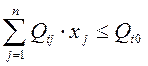
Запишем  формулу   в  канонической  форме

                                                              

                                                                                                           

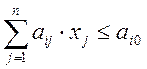
Для  канонической  формы  широко  известен  симплекс  метода  (,  если  умножить  правую  и  левую  часть  неравенства  на  ,  то  знак  неравенства  меняется  на противоположный  ).

Если  не  все  переменные   подчинены  условию  неотрицательности,  то  их  можно  представить  в  виде  разности  двух  переменных.

      

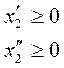
Задачу  поиска  минимума  можно  заменить   поиском  максимума,  если  правую  или  левую  часть  умножить  на  .

Задача  о  раскрое.

К  этому  виду  задач  относятся  задачи  оптимального  раскроя  материала.

Постановка  задачи.  Имеется  материал  определенной  формы.  Из  данного  материала  необходимо  вырезать  заготовки  з1,  з2, …,зn.  Даны  возможные  варианты  раскроя  .  Дано  количество  заготовок,  каждого  вида  которые  можно  вырезать  из    материала  и  количество  отходов  полученных  по    этому  варианту  раскроя  (i- номер  заготовки,  j– номер  варианта  раскроя).

Согласно  плану  нам  необходимо  заготовок  з1  не  менее  b1  штук

.

Необходимо  обеспечить  план  выпуска  изделий,  в  состав  которых  входят  заготовки  з1, з2, …, зn  в  количестве  N1, N2, …,Nm.  Количество  материала  взятого  в  раскрой  по  каждому  из  вариантов  не  может  быть  отрицательным.

Пример  задачи  о  раскрое.

Из  уголка  длинной  5  метров  требуется   нарезать  заготовки  длиной  3  метра -   20  штук,  длиной  1,8 метров – 100  штук.  Необходимо  получить  минимум  отходов,  максимум  заготовок.

├──── 5 метров ──────┤                                   отходы

           0,2 - метров

1)  ├── 3 метра ────┤                           0,2 - метров

         1,4 - метров

2)  ├── 2,4 метра ──┤                               0,8 - метров

3)  ├─ 1,8 метров ─┤

№ полосы	Количество  заготовок			Отходы, м
	1	2	3
1	1	-	1	0,2
2	-	2	-	0,2
3	-	1	1	0,8
4	-	-	2	1,4
План	20	60	100

, где  - количество  исходных  полос,  разрезанных  - м  раскроем.

Определяем  суммарное  число  полос  разрезанных  каждым  вариантом.  Заготовки  первого  вида  мы  можем  получить  только  при  первом  варианте  раскроя                                     

Заготовки  второго  вида  мы  можем  получить  вторым  и  третьим  вариантами  раскроя