![]()
Поэтому, если окажется что это равенство не выполняется, то это является первым признаком наличия стохастической зависимости между X и Y. Часть стохастической связи между X и Y, которая сказывается на отличии левой части от правой, называется корреляция. Необходимым и достаточным условием корреляции служит неравенство:
![]()
Коэффициент корреляции определяется по формуле:
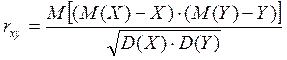 , а числитель этой дроби
называется корреляционным моментом.
, а числитель этой дроби
называется корреляционным моментом.
Рассмотрим основные свойства коэффициента корреляции:
1. ![]()
![]()
2. ![]()
Связь между величинами X, Y можно
описать линейной функцией. Если модуль ![]() описывается
квадратной функцией
описывается
квадратной функцией ![]() . Если
. Если ![]() ,
то величины X, Y не описываются удовлетворительно максимальной
зависимостью. Если
,
то величины X, Y не описываются удовлетворительно максимальной
зависимостью. Если ![]() , то эти величины являются
независимы.
, то эти величины являются
независимы.
Для системы двух СВ X иY измеренные данные можно представить в виде корреляционной таблицы.
Таблица 1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
В этой таблице значение ![]() - значение, которое принимает СВ x;
- значение, которое принимает СВ x; ![]() - значения, которые принимает СВ y. Один опыт характеризуется изменением величин X и
Y
- значения, которые принимает СВ y. Один опыт характеризуется изменением величин X и
Y ![]() . Не исключается, что в некоторых опытах
будут встречаться те же самые значения X и Y. Величины
. Не исключается, что в некоторых опытах
будут встречаться те же самые значения X и Y. Величины ![]() описывают частоты
встреч ситуации, когда X и Y принимают определенное значение;
описывают частоты
встреч ситуации, когда X и Y принимают определенное значение; ![]() - описывает сколько раз среди всех
проводимых опытов встретилась ситуация, когда
- описывает сколько раз среди всех
проводимых опытов встретилась ситуация, когда ![]() . В
последнем столбце
. В
последнем столбце ![]() - сумма по всем величинам
- сумма по всем величинам
![]()
Сумма всех частот
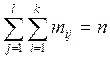
Таким образом, каждому
значению ![]() соответствует распределение значений
соответствует распределение значений ![]() с некоторыми частотами
с некоторыми частотами ![]() .
.
Пример Исследуется пассажиропоток для определенного маршрута троллейбуса
x - номер остановки,
y – количество пассажиров в троллейбусе на этой остановке.
Цель расчета: построить теоретическую зависимость y и x , чтобы обосновать необходимость строительства на некотором промежутке остановки. По результатам измерений получены значения.
Таблица 2
|
|
0 |
1 |
… |
60 |
|
|
1 |
10 |
15 |
… |
2 |
|
|
2 |
7 |
10 |
… |
1 |
|
|
|
|
|
|
|
|
|
10 |
2 |
4 |
… |
7 |
|
|
|
|
|
… |
|
n |
Подсчет ведется в течение одного дня. За это время троллейбус много раз проезжает по кольцу. Числа в таблице означают, что на 2 остановке пассажир 1 встречается 10 раз. В результате расчетов будет найдена зависимость Y(X). Эта зависимость позволяет получить данные по тем областям, где отсутствует эксперимент и выполнить аппроксимацию.
Берем среднее значение для каждого X.
Таблица 3
|
X |
X1 |
X2 |
… |
Xk |
|
|
|
|
… |
|
|
частота |
|
|
… |
|
Среднее значение вычисляется по строке. Для X2:
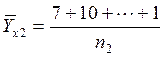
Таким образом, между X и
средним значением Y среднее по X существует
функциональная зависимость ![]() (*)
(*)
Аналогично вычисляя по столбцу можно построить таблицу
|
Y |
|
|
… |
|
|
|
|
|
… |
|
|
частота |
|
|
… |
|
Для ![]() :
:
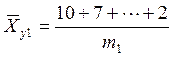
Если между величиной Y и
![]() имеется некоторая зависимость, то имеет
место стохастическая или корреляционная связь между X и
имеется некоторая зависимость, то имеет
место стохастическая или корреляционная связь между X и ![]() :
:
![]() (**)
(**)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.