Основные понятия моделирования. Виды моделирования. Этапы создания модели. Задачи математического программирования, страница 6

В данном случае мы решали задачу линейного программирования.

Существуют и другие решения задачи о загрузки печи.

Вместо стоимости можно выбрать другие характеристики. Например,  сложность приобретения  заданного ингредиента.

Задача (пример).

Подготовить состав смеси наиболее подходящий к заданному процентному уровню содержащегося элемента. В этом случае цены на ингредиенты нет и нет значимости ингредиента.

Пусть  A=(aij) матрица содержания элементов в ингредиентах.

P – вектор  требуемого  состава  в  процентах,  тогда  если

  вариант  загрузки  печи

-  на 100% загружена  печь

Получим F- вектор фактического процентного содержания элементов в печи.

  

    Цель: минимизировать различие фактического содержания  в печи элементов  от  заданного  ограничения.

Сформулируем задачу для решения в MathCAD.

Найти такой вариант значений  , при котором данная разность является минимальной при заданных ограничениях.

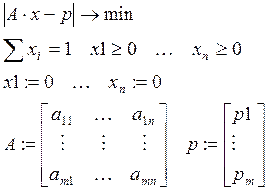
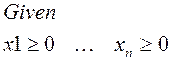
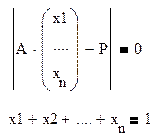
Основные понятия теории вероятности и

 математической статистики.

Основные понятия теории вероятности (ТВ).

     Событием в ТВ называется факт, который может произойти или не произойти в результате некоторого испытания (отказ компьютера в момент включения).

Для каждого испытания можно указать некоторую совокупность или множество взаимоисключающих элементарных событий, причем в результате испытания может произойти только одно из них. Такая совокупность называется пространством элементарных событий.

     Пример: 2 раза бросаем монетку: в этом случае пространство событий содержит 4 элемента.

-частотой случайных событий А  данной серии испытаний называется отношение числа испытаний к общему числу испытаний.

 

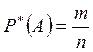
m-число событий, которое произошло.

n-число испытаний.

   Вероятностью случайного события А называется некоторое число, около которого группируется частота этого события, по мере увеличения количества испытаний. Статистическое определение вероятности событий:

P(a)=m/n

m -благоприятные исходы

n-вероятность события

     Основные свойства вероятности:

1.  вероятность случайного события  А есть неотрицательное число от 0 до 1.

2.  вероятность достоверного события равна 1.

3.  вероятность невозможного события =0.

4.  условной вероятностью события А по отношению к событию В называется вероятность наступления события А, вычисленная при успешном наступлении события В.

P(A/B)- вероятность наступления события А при условии что произошло В.

5.  два события называются зависимыми, если вероятность любого из них меняется с наступлением другого, в противном случае они независимы.

Для независимых событий вероятность события А или В равна в сумме вероятности А и В.

P(A+B)=Р(А)+Р(В)        

Р(А*В)=Р(А)*Р(В)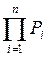         

Сумма вероятности событий образующих полную группу =1.

Вероятность не наступления события:

Для совместных событий:

Р(А+В)=Р(А)+Р(В)-Р(А)*Р(В)

Р(А*В)=Р(А)*Р(В)

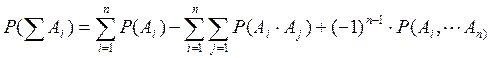
Пример:

При приемке партии производится проверка половины изделий. Условие приемки допускает не более 2% брака. Определить вероятность того, что партия из 100 изделий, содержащая часть бракованных будет принята.

Решение:

Условие приемки - 2% брака. Проверяется половина партии, допускается не более 1 бракованного изделия.

Событие А – при проверке не обнаружено бракованное изделие.

Событие В -  при проверке обнаружено одно бракованное изделие.

Условие приема партии наступит либо событие А либо событие В.

Р(А+В)=Р(А)+Р(В)=0.18

Для первого случая из 100 изделий 50 можно выбрать следующим числом способов:

    ,    

Р(А)=              Р(В)=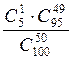     

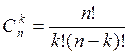
Случайная величина Х может быть задана дискретным или   непрерывным распределением.

Если случайная величина может принимать конечное множество значений, то ее будем называть случайной дискретной величиной. В противном случае  непрерыв-  ной. Случайные дискретные величины задаются таблицей распределения.

Пример:

Xi	X1	X2	….....	Xn
Pi	P1	P2	…….	Pn

Xi - возможное значение случайной величины

Pi – соответствующая им вероятность

Число бракованных изделий в партии из 5 штук может принять ряд значений