Основные понятия моделирования. Виды моделирования. Этапы создания модели. Задачи математического программирования, страница 16

loess(VX,VY,Span) возвращает вектор требуемой функции interp, чтобы найти набор полиномов 2-го порядка, которые наилучшим образом приближают заданные окрестности опытных точек определённых векторами VX и VY.

Аргумент span>0 определяет насколько большие окрестности опытных точек задаются.

inter(VS,VX,VY,X) – возвращает интерполяцию значений Y соответствующих значениям Х.

Вектор VS вычисляется с помощью функций loess или regress на основе опытных данных занесенных в вектора VX и VY.

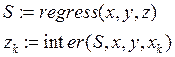
Т.к. regress пытается приблизить все точки данных одним полиномом, то она не дает точного результата для данных несвязанных единой полиномиальной зависимостью. В этом случае используется функция loess, позволяющая выполнить аппроксимацию с помощью нескольких полиномов.

Аргумент span рекомендуется задавать порядка 0,50,75

Пример:

I := 0,…49

VX_i := i

опыт

span = 0,3

VS := loess(VX,VZ,span)

f(x) := interp(VS,VX,VZ,x)

VXi

Оптимизация в среде EXCEL

1.  Рабочая таблица.

2.  Базы данных (EXCEL).

3.  Диаграмма (позволяет строить графики, диаграммы и т.д.).

Рабочую таблицу можно представить как электронный план документа, граф и  строки, которые связывают формулы.

Рабочие таблицы объединены в книгу. Книга хранится в виде файла на диске и имеет расширение xls. Книга может содержать от 1 до 256 таблиц рабочих, которые называются листами.

	A	B	C	…
1
2
3
…

Столбцы A, B, C до буквы Z, затем идет АА, ВВ и т.д. всего их 256. Строк примерно 65000.

Каждая клетка имеет свой номер.

Область В1:С4; А1.

Ввод данных

Базовые операции:

< 

<=

> 

>=

<> 

=

& конкатенация (слияние текста).

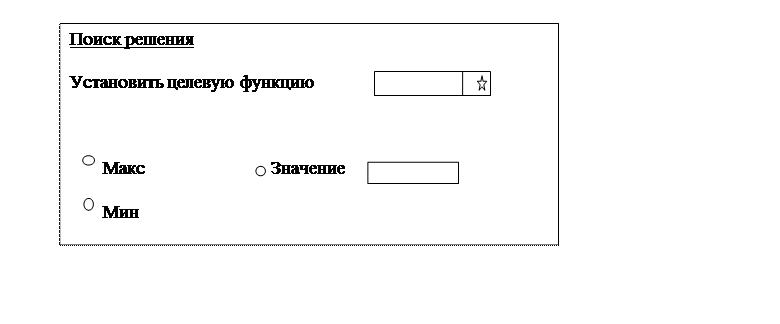
EXCEL позволяет решать задачи оптимизации, но для этого необходимо активизировать средства поиск решения (Сервис – Настройка – Поиск решения).

Решение задачи раскроя

	A	B	C	D	E	F	G	H
1		Вариант 1	Вариант 2	Вариант 3	Вариант 4	Факт	План	Отклонение
2	Заготовка А	4	3	1	0	0	180	F2-G2
3	Заготовка В	0	3	9	12	0	900	F3-G3
4	Отходы	12	5	3	0	0
5	Количество	1	1	1	1

1=B2*B5+C2*C5+D2*D5+E2*E5

2=   3           3            3            3

3=   4           4            4            4

Сервис         Поиск решения

Модели регрессионного анализа

1.  Модель одномерного регрессионного анализа

В одномерном анализе на результаты Y воздействует только 1 фактор Х. Мы предполагаем наличие связи между выходом и входом.

	Х

 

Пример связей: Y=2X – линейная связь

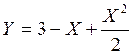  - квадратичная связь может создаваться полиномом n-ой степени.

Нам необходимо определить эту связь на основании опытных данных.

Методика решения:

1.  Проводим эксперимент с n опытами, где  для каждого значения Х изменяем выходное значение Y. Результаты оформляем в виду таблицы:

Х1	Х2	…	Хn
Y1	Y2	…	Yn

2.  Подбираем вид зависимости Y от Х , для этого:

1) подготавливаем график зависимости  Y от Х ;

2)  рассчитываем коэффициент корреляции;

3) определяем значимость коэффициента корреляции;

4) рассчитываем коэффициент детерминации;

5) по коэффициенту детерминации определяем степень зависимости Y от Х;

6) определяем вид уравнения (вид зависимости, используется график и коэффициент детерминации);

7) рассчитываем коэффициенты уравнения регрессии.