Основные понятия моделирования. Виды моделирования. Этапы создания модели. Задачи математического программирования, страница 3

═ ,  (═  (ctrl=)).

 Find ()

Пример                                            

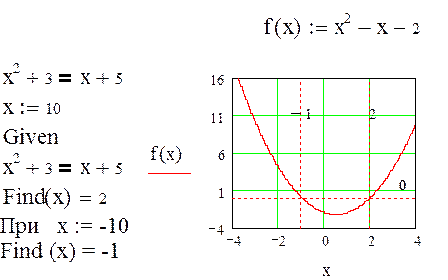
При поиске корней MathCAD может выдать: solution not found (решение  не найдено)

Когда решение не найдено,  требуется:

а) изменить значение начальной точки;

б) ввести ограничение.

3.Решение уравнений – полиномов.

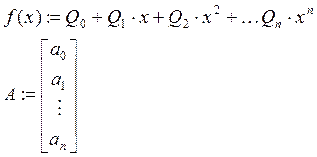
Пример

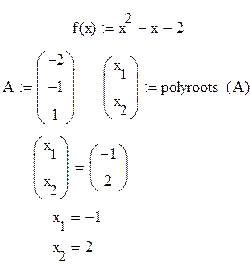
4.  Системы линейных уравнений.

                             

                 

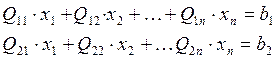
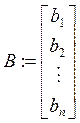
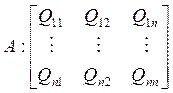
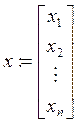
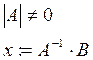
Пример

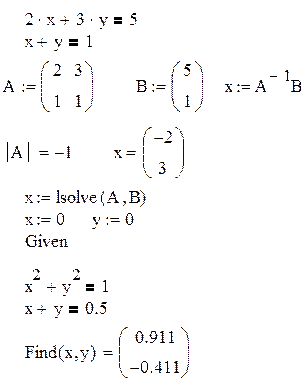
Оптимизация. Основные понятия.

(управляемое  воздействие)

F(x) система

                                                          ↓ 

 ¾®                              ¾® 

(неуправляемое

воздействие)                                        

                                              (случайное  воздействие)       

Позволяет проводить анализ, получать оценки выходных данных на основе различных входных воздействий, сравнивать их между собой, выбирать те которые обеспечивают наилучший результат.

Процесс поиска наилучшего решения, называется  оптимизацией, при этом формулируется понятие “наилучшее решение” приводит к необходимости задания предпочтения, на основании, которого одно решение считается лучше, чем другое.

Основой предпочтения выбирается численное решение объекта, характеризуется уровень эффективности данного решения. Данная характеристика, как правило, является функцией зависящей от определенных параметров. Этими параметрами является  управление воздействия , т.к. изменяя, их мы можем изменять поведение объекта. Задача параметрической оптимизации заключается в выборе таких значений управляемых параметров , которые обеспечивали бы экстремальное (самое лучшее) значение характеристической функции. Параметрическая функция, экстремум которой мы получили, называется – целевой функцией.

Параметры, обеспечивающие экстремум целевой функции называют, экстремумами. Если целевую функцию обозначить буквой , то решение ищется в  мерном пространстве вектора .

Функцию  часто называют функцией отклика на воздействие  .

-это вектор из  элементов.

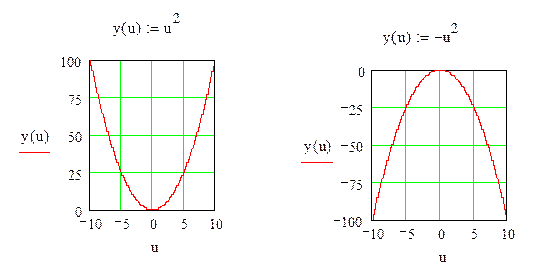
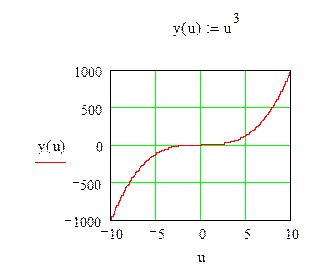
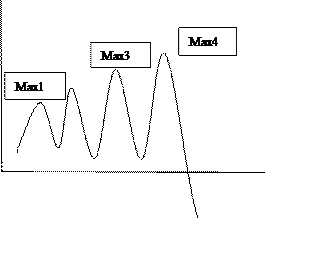             имеет множество решений.      

Если экстремум ищется в неограниченной области, то такой экстремум называется – безусловленным, соответственно методы его поиска методы безусловной оптимизации. Если присутствует ограничение соответственно методы условной оптимизации.

Область, которая удовлетворяет ограничениям, называется допустимой областью или областью допустимых значений.

↓                                          Если  в  модели  черного  ящика  убрать                                     

                                                              случайное  воздействие  ,  то  задача                                         

 ¾®                    ¾®                 сведется  к  подбору  таких  значений  , которые  обеспечивают  экстремум  .         

Задачи математического программирования.

Постановка задачи математического программирования.

 Математическое  программирование (МП) – область  математики,  разрабатывающая  теорию  и  численные  методы  решения  многоэкстремальных  задач  с  ограничениями.

Постановка  задачи.  Требуется  найти  значение    переменных  ,  которые  удовлетворяют    уравнениям  или  неравенствам.

                                                      

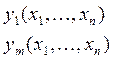
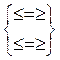
Позволяет  минимизировать (максимизировать)  функцию      

Условие   называется  ограничениями,   - целевая  функция.

В  данной  постановке  полагается  что

                   

Вид  функции    известен.  Число  переменных    и  число  уравнений    никак  между  собой  несвязаны.  Любые  ограничения  отсутствуют,  кроме  того,  часто  на  некоторые  ограничения  накладываются  специфические  условия:

1.  неотрицательность

2.  дискретность

В  зависимости  от  вида  функции    и    различают  задачи:

a)  линейного  программирования  ( все  функции  линейно  относительны  )

б)  нелинейного  программирования  (хотябы  одна  из  функции  нелинейна)

в)  динамического  программирования.