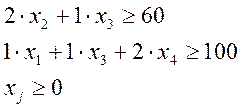
Кроме того, количество заготовок не может быть отрицательным.
Задача в общем виде
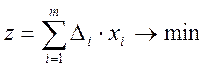 , где
, где ![]() -
отход при iварианте
раскроя или при
ограничениях
-
отход при iварианте
раскроя или при
ограничениях
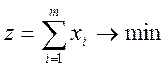
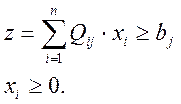
![]()
Задача о смесях.
Смеси в нефтяной, медицинской промышленности.
Цель: получить смесь с заданными свойствами при наименьших затратах на исходные сырьевые ресурсы.
Смесь имеет
ингредиенты ![]() , которые содержат различные элементы
, которые содержат различные элементы ![]() . Единица
. Единица ![]() го
ингредиента стоит
го
ингредиента стоит ![]() .
. ![]() - количество
микроэлемента i в jингредиенте. Смесь должна содержать не менее
- количество
микроэлемента i в jингредиенте. Смесь должна содержать не менее ![]() микроэлемента
микроэлемента ![]() ,
…,
,
…, ![]() микроэлемента
микроэлемента ![]() .
.![]() - количество j
ингредиента взятого для приготовления смеси.
- количество j
ингредиента взятого для приготовления смеси.
|
Ингредиент |
1 |
2 |
… |
m |
b |
|
|
|
… |
|
||
|
Микроэлемент 1 |
2 |
10 |
… |
… |
|
|
Микроэлемент 2 |
5 |
3 |
… |
… |
|
|
………………… |
… |
… |
… |
… |
|
|
Ингредиент m |
… |
… |
… |
… |
|
|
Стоимость ингредиентов |
|
|
… |
|
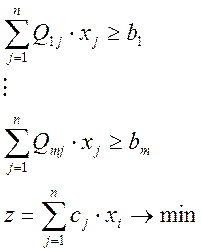
Решение задач оптимизации в системах MathCAD.
Решение классических задач поиска экстремума в MathCAD.
В поисках экстремума используется блок решения (Given, Find). Для поиска экстремума необходимо взять производную и приравнять ее к нулю.
Пример
Дана функция
![]() . Требуется найти ее экстремум.
. Требуется найти ее экстремум.
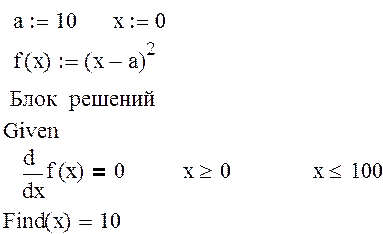
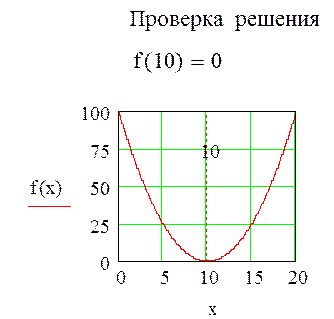
Экстремум функции от двух переменных.
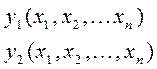
![]()
…………………………………
В этом случае решение производят аналогично предыдущему случаю, но без графика.
Пример
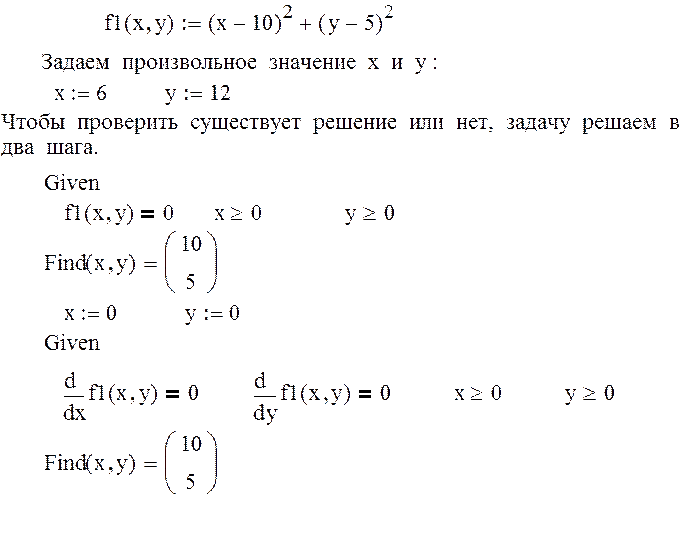
Во многих случаях первый шаг можно опустить.
Задача о смеси.
Составить наиболее дешевую смесь из трех ингредиентов (1 2 3), с содержанием не менее 6 единиц элемента A, 8 единиц - B и 12 единиц - С.
|
1- x1 |
2-x2 |
3-x3 |
фактическое |
план |
ограничение |
|
|
Элемент A |
2 |
1 |
3 |
= |
6 |
|
|
Элемент B |
1 |
2 |
1,5 |
= |
8 |
|
|
Элемент C |
3 |
4 |
2 |
= |
12 |
|
|
цена |
2 |
3 |
2,5 |
= |
![]()
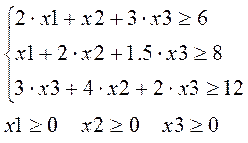
![]()
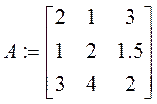
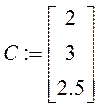
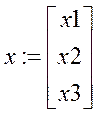
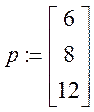
Целевая
функция ![]()
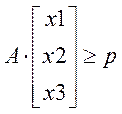
Пример
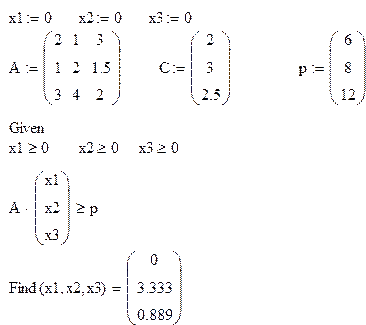
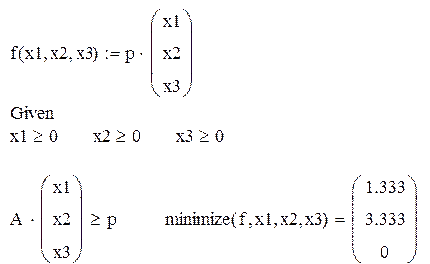
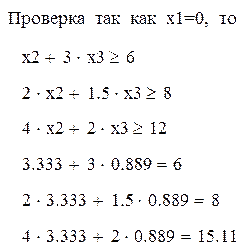
Задача о раскрое
Пример 1
Из листового материала определенной формы необходимо вырезать заготовки двух видов: A и B для выпуска 90 единиц изделий. На каждое изделие требуется 2 заготовки A и 10 заготовок B.
|
Вид заготовки |
X1 |
X2 |
X3 |
X4 |
План |
ограничения |
|
A |
4 |
3 |
1 |
0 |
180 |
|
|
B |
0 |
3 |
9 |
12 |
900 |
|
|
Отход |
12 |
5 |
3 |
0 |
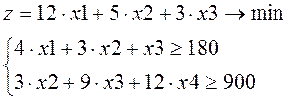
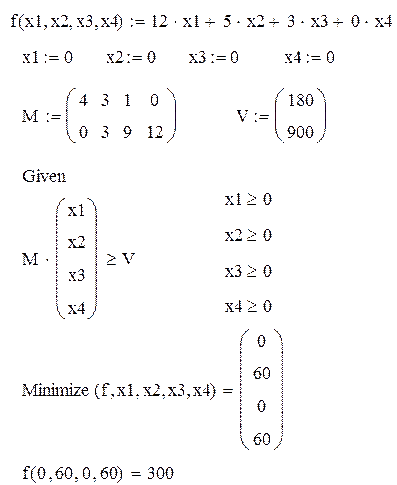
Пример 2
Необходимо нарезать заготовки труб длиной 20, 25 и 30 единиц из прудка длиной 75 единиц. При этом требуется заготовок первого вида – 300, второго вида 270, третьего – 350. Требуется определить количество прудков, которое обеспечивает выполнение плана и при этом длина отходов минимальна.
|
Трубы |
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
План |
|
1 типа |
3 |
1 |
1 |
0 |
2 |
0 |
300 |
|
2 типа |
0 |
2 |
1 |
0 |
0 |
3 |
270 |
|
3 типа |
0 |
0 |
1 |
2 |
1 |
0 |
350 |
|
отход |
15 |
5 |
0 |
15 |
5 |
0 |
min |
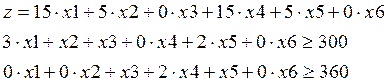
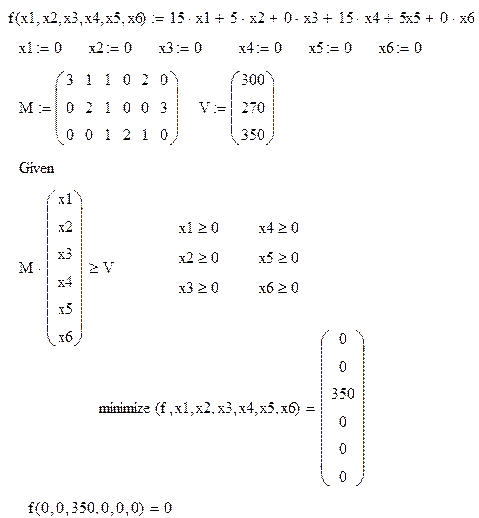
Задача о загрузке печи.
Вариант 1. Составить наиболее дешевую смесь.
Пусть Aij – процентное содержание i– го элемента в j – ом ингредиенте.
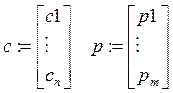
Цель формируется следующим образом:
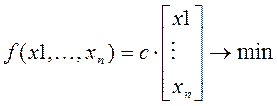
либо ![]()
При заданных ограничениях:
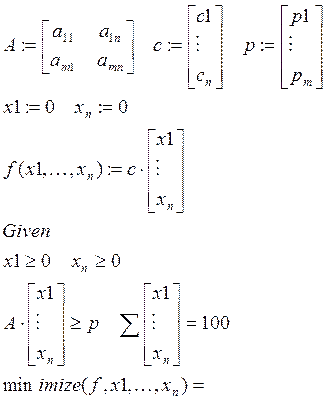
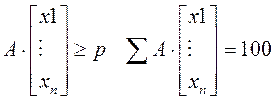
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.