Основные понятия моделирования. Виды моделирования. Этапы создания модели. Задачи математического программирования, страница 8

Прямая задача заключается в определении вероятности попадания СВ в заданный интервал по известной функции f(x) и величине заданного интервала.

Существует 3 вида прямых задач:

P(X<x);         P(X>x);             P(X1<x<X2).

1.Найти вероятность попадания случайной величины в интервал ограниченный от до x.                                                                                                                                                                           

В этих задачах известна функция распределения случайной величины, известен интервал.

Задача: найти вероятность попадания СВ в заданную области.

Обратная задачавытекает из прямой. Известна вероятность попадания СВ в заданный интервал P(X<x)=p.

Требуется найти либо функцию распределения F(x) либо интервал.

P(X1<x<X2)=p   X1-? X2-? (p-известно, надо найти Х)

 

Задача имеет множество решений

Х

Законы распределения случайных величин.

1.  Среди непрерывных СВ наиболее простое выражение для плотности вероятности имеет равномерный закон.

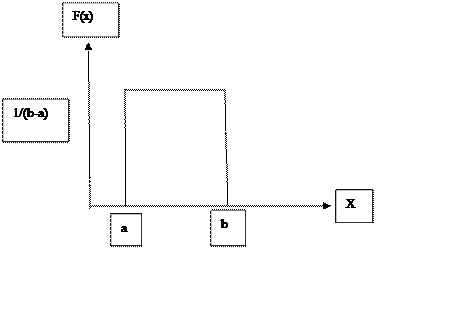
f(x)=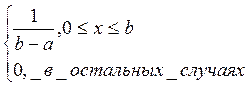

Равномерный закон распределения – все числа равны вероятным.

Свойства равномерного распределения:

1) Математическое ожидание.

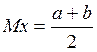
2) Дисперсия.

Dх =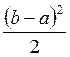

3) Среднеквадратичное ожидание.

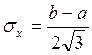
4) Вероятность попадания СВ в интервал.

<x<,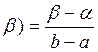

не включая.

В MathCADесть встроенные  и  функции для этого закона распределения:

1. rnd (x) – возвращает случайную величину, равномерно распределенную на         интервале  , если надо , то 100rnd(x).

      2. dunif (x,a,b) – возвращает плотность распределения, т.е. отношение вероятности того, что случайная величина попадает в малый диапазон с центром в данной точке к величине данного диапазона (плотность распределения).

4. punif (x,a,b)- возвращает функцию распределения.

5. qunif (p,a,b)-возвращает функцию обратную функции распределения.

6. runif (m,a,b) – возвращает вектор из m случайных чисел, равномерно распределенных на интервале а, в.

unif- обозначает равномерное распределение.

Биноминальный закон распределения Пуансона.

Биноминальный закон распределения имеет место в том случае, когда случайная величина Х выражает число появлений  некоторого события А при n              независимых испытаний проводимых в одинаковых условиях. Вероятность появления события А постоянна и равна p.

Возможными значениями случайной величины х являются числа 0,1,2,…,n, а вероятность того, что х = k определяется формулой:

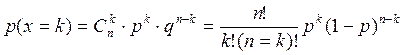 , q = 1 - p .

Математическое ожидание  СВ х,  распределенной по биноминальному закону

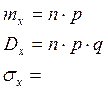
dbinom(x,n,p)   - возвращает плотность биноминального распределения;

pbinom(k,n,p) – возвращает функцию биноминального распределения;

qbinom(p,n,r) – возвращает функцию, обратную первой;

zbinom(m,n,p) – возвращает вектор.

Распределение Пуассона

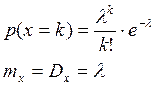
Биноминальный закон распределения сводится к распределению Пуассона, когда

dpois(k,

ppois (k,

qpois(p,

zpois(m,

Нормальный закон распределения

Непрерывная СВ х распределяется по нормальному закону (Гаусса), если ее плотность вероятности равна:

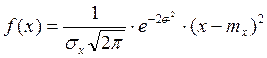, где - математическое ожидание;

- среднее квадратичное отклонение.

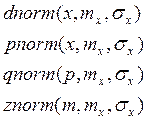
m- число элементов вектора.

Кроме того, для нормальных законов существует cnorm(x) – эта функция возвращает функцию ,

Функция симметрична относительно математического ожидания и распределена на интервале от до .

Распределение

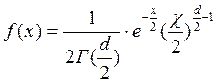
d- число степеней свободы;

Г – гамма функция из таблицы.

dchisg(x, 1, s)

pchisg( x, s1,s2)

qchisg(p,n)

zchisg(m,d)

Критерий Пирсона

Критерий Пирсона применяется для проверки правдоподобия гипотез. Противоречат ли опытные данные гипотез о том, что случайная величина х распределена по такому-то закону. Для ответа на этот вопрос пользуются так называемыми критериями согласия: критерий Колмогорова и критерий Пирсона.

Пусть х – дискретная СВ с возможными значениями х1,х2, …, хк.

Предположим, что произведено n независимых опытов, в каждом из которых СВ приняла определенное значение. На основе этих опытов составим статистический ряд распределения: