Основные понятия моделирования. Виды моделирования. Этапы создания модели. Задачи математического программирования, страница 7

X1=0…..5

Введем понятие закона распределения СВ.

Законом распределения СВ называется любое соотношение (правила, таблица, функция), устанавливающее связь между возможным значением случайной величины и соответствующей ему вероятностью.

Функцией распределения случайной величины Х называется функция F(x) равная вероятности того, что случайная величина будет меньше произвольно выбранного значения Х.

F(x) =P(x<X)

Для случайных непрерывных величин большое значение играет понятие плотности распределения СВ.

Плотностью распределения непрерывной СВ точки Х называется производная ее функции распределения в точке Х.

               

а

а

х

                                                           

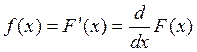
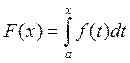
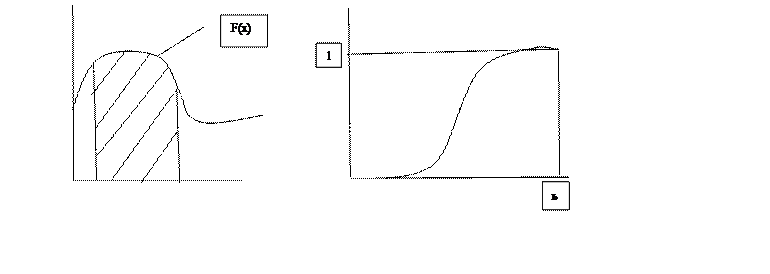
1. F (a) =0.

2. F (b) =0.

3. X2>X1 – неубывание. 

F(X2))

4. P(X1<X<X2)=F(X2)-F(X1)   

Вероятность попадания СВ в заданный интервал Х1<X<X2:

P(X1<X<X2)=

Характеристика случайных величин (СВ)

1.  Математическое ожидание М(х)

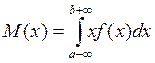
Для случайной дискретной величины

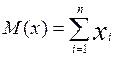
Свойства математического ожидания

1.  М(с) = с, где с = const;

2.  ;

3.  М(с+х) = с+М(х);

4.  М (х+у) = М (х)+М(у), где х, у – случайные величины;

5.  , если х и у независимы;

2.  Дисперсия

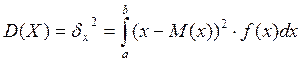 - длянепрерывной СВ

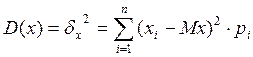  - для дискретной случайной величины

3.  Среднеквадратичное отклонение 

 

Свойства среднеквадратичного отклонения

1.  D(с) = 0;

2.;

3. D(c+x) = D(x);

4.  D(x+y) = D(x)+D(y), если х и у независимы;

4.  Коэффициент корреляции

Корреляция-связанность

1.

2. Если , то между х и у существует функциональная линейная связь

у=ах+b

Чем ближе по модулю коэффициент корреляции К1, тем ближе связь к линейной , тем сильнее связаны случайные величины.

3.Если , то случайные величины х и у не связаны.

5.  Коэффициент детерминации  

                          

1.  bху = 1 – линейная связь между х и у;

2.  bху > 0,9 – сильная связь, близкая к линейной;

3.  bху = 0,8 – означает, что 80% всех ситуаций можно объяснить наличием связи между х и у и только 20% - это влияние неизвестных нам факторов.

	F

 

                                         80%х                                                                    х

 

20%z – неизвестные факторы

4.  - имеет смысл строить модель.

В остальных случаях необходимо доопределить влияние изучаемых факторов и выделить их значение.

Основные понятия математической статистики

Пусть Х – случайная величина с законом распределения F(x) (либо с плотностью f(x)). Назовем генеральной совокупностью все мыслимое количество испытываемой величины.

Выборкой назовем конечную выборку из генеральной совокупности Х1…Хn.

Если совокупность конечных значений выборки Х1…Хn расположить в возрастающем порядке, то получим статистический ряд.

Если статистический ряд разделить на интервалы

, то  каждое из значений Х попадает в один из интервалов .   

                               

                                      

Пусть hk -  количество значений из выборки, попавшее в к-ый интервал, тогда

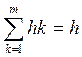   это и есть объем выборки. Величина hk называется частотой, а вектор Н называется гистограммой частот.

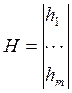
Величина 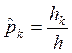      называется частостью или эмпирической вероятностью. Она характеризует вероятность попадания СВ х в k-ый интервал.

При очень большом объеме выборки n  стремится к бесконечности. Эмпирическая вероятность будет стремиться к теоретической. Статистический ряд, заданный в виде интервалов 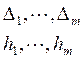 и частостями    называется интервальным статистическим рядом.

Характеристики выборки x

1. Оценка выборки 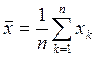   x-среднее значение, аналог математического ожидания.

2. 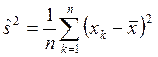-оценка дисперсии.

3. Оценка среднеквадратичного отклонения  .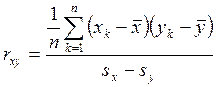

4. Оценка теоретического коэффициента корреляции

4. Прямые и обратные задачи.