Основные понятия моделирования. Виды моделирования. Этапы создания модели. Задачи математического программирования, страница 10

1. 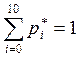- условие совпадения математического ожидания.

Итого получим d=11-2=9.

Для полученных значений d=0, .

Находим p=0.1- значение нашего критерия. А далее сравниваем:  сравниваем с 0.1.

Получаем 0.1<0.15, это значит что гипотеза о соответствии распространения СВ Х по Пуассоновскому закону противоречит опытным данным и ее необходимо отбросить.

  Проверка  гипотез  в  MathCAD.

Функции  для  расчета  статистик,  их  3.

1.  mean(x),  где  x – вектор.

 

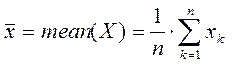
2. Дисперсия

3. Среднеквадратичное  отклонение

4.  length(x)

5.  hist(Intervals, Data) оба  параметра  вектора.

           Intervals  -  вектор  интервалов

Data – вектор  данных

Данная  функция  возвращает  вектор,  который  показывает,  сколько  значений  из  вектора  Data  попало  в  соответствующий  интервал.

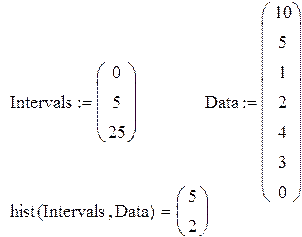
Длина  вектора  hist на  единицу  меньше  длины  вектора  Intervals.

6.  Ввод  данных  в  MathCAD.

Создание  файла  данных  в  Dows,  с  помощью  shift  F4  вводим  числа,  затем  данные  сохраняем (F2).  После  создания  файла  необходимо  ввести  его  в  MathCAD.

Ввод  структурных  данных  ,  далее  в  меню  файл  выбираем   опцию  Associativ,  далее  имя  своей  переменной  filename.

Критерий  Пирсона  предназначен  для  проверки  соответствия  распределения  выборки  заданному  теоретическому  распределению.

Мы  будем  проверять  на  соответствие  нормальному  распределению,  хотя  он  используется  и  для  других  распределений.  Основная  идея  проверки: если  распределение  выборки  и  заданное  (в  нашем  случае  нормальное)  распределение  совпадают,  то  должно  выполняться  условие   (F наблюдаемое  меньше  чем  F критическое).

Алгоритм  проверки  состоит  из  следующих  шагов:

1.  Подготовить  выборку

2.  Рассчитать  общие  статистические  характеристики  (среднее  значение, среднеквадратичное  отклонение,  размер  выборки)

3.  Привести  выборку  к  нормализованному  виду;

4.  Рассчитать  вектор  эмпирических  частот;

5.  Рассчитать  вектор  теоретических  частот;

6.  Рассчитать  наблюдаемое значение  критерия (Fnabl);

7.  Рассчитать  критическое  значение  критерия  (Fkr);

8.   Принять  решение. Если  Fnabl<  Fkr,то  соответствует (различие незначительно), в  противном  случае  несоответствует (различие  значимо).

Расчетные  формулы

1.  Вводится  выборка

2.  Рассчитываем  статистические  характеристики

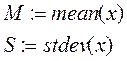
 - размер  вектора  x.

3.Приводим  выборку  к  нормализованному  виду  по  формуле

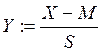
4. Находим  вектор  эмпирических  частот

                                                   

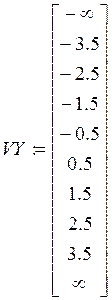
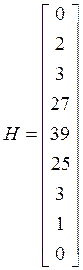
5. Рассчитать  вектор  теоретических  частот

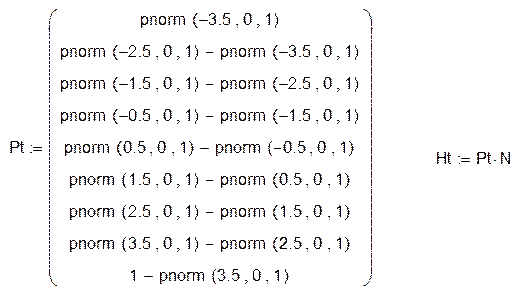
Альтернативный  способ  получение  вектора  теоретических  частот

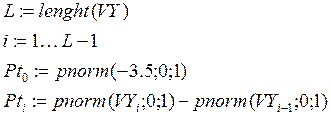
6.  Рассчитаем  наблюдаемое  значение  критерия

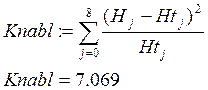
7. Рассчитаем  критическое  значение  критерия

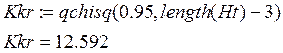
8.  Принимаем  решение.  Так  как  Knabl  <  Kkr ,  то  гипотеза  принимается.

Основные  понятия   дисперсионного  анализа (ДА). 

Однофакторный  диффузионный  анализ  (ОДА).

 Схема  применения  модели  ОДА.

    ДА – область  статистических  моделей,  которая  занимается  выявлением  влияния  различных  факторов  на  исследуемые  величины  или  признаки  A→x                                                   

(A  влияет  на  x). ДА  позволяет  установить  степень  влияния  факторов  Aна  изменчивость  исследуемого  признака  x.  При  этом  можно  установить  лишь  наличие  исследуемого  влияния.  По  количеству  факторов  выделяют  однофакторный,  двухфакторный,  трехфакторный  анализ.

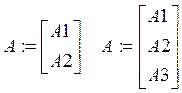
Влияние  изучаемых  факторов  может  быть  двояким.  Эти  факторы  могут  изменять  как  истинный  результат  (среднее  значение  величины  x).

За  истинное  значение  принимается  среднее  арифметическое.

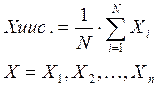
Могут  влиять  на  дисперсию (разброс).

Мы  будем предполагать, что  дисперсия  наблюдений  остается  неизменной.  Это  предположение  оправдывается  тем,  что  для  наблюдений  используется  одна  и  та  же  методика.  Идея  дисперсионного  анализа  состоит  в  том,  что  дисперсия  признака  x  или  разброс  случайной  величины  x  разлагается  на  сумму  составляющих  ее  дисперсий.