|
Х1 |
Х2 |
Х3 |
… |
Xi |
… |
Xk |
|
P1* |
P2* |
P3* |
… |
Pi* |
… |
Pk* |
Где
Pi* = ![]() - частота события;
- частота события;
![]() - число опытов, в которых появилось это
событие.
- число опытов, в которых появилось это
событие.
Мы выдвигаем гипотезу Н о том, что СВ х имеет ряд распределения
|
Х1 |
Х2 |
… |
Хi |
… |
Xk |
|
P1 |
P2 |
… |
Pi |
… |
Pk |
А отклонение частот Pi* от вероятности Piимеет случайные причины. Чтобы
проверить правдоподобие этой гипотезы, необходимо выбрать некоторую меру
расхождений статистического распределения с гипотетическим. В качестве меры
расхождения R с гипотетическим распределением 2 и статистическим
1. При использовании критерия Пирсона берется сумма квадратов отклонений Pi*-Pi,
взятых с некоторым коэффициентом ![]()
![]()
Коэффициент ![]() вводится потому, что отклонение,
относящееся к разным Piнельзя
считать равноправным по значимости. Одно и тоже отклонение (по абсолютной
величине) может быть малозначимым, если велика сама вероятность Pi
, и значимым, если она мала.
вводится потому, что отклонение,
относящееся к разным Piнельзя
считать равноправным по значимости. Одно и тоже отклонение (по абсолютной
величине) может быть малозначимым, если велика сама вероятность Pi
, и значимым, если она мала.
Пример:
Р1=0,98
Р1*=0,97
Пирсон доказал, что если 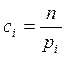 , то при больших
значениях nзакон
распределения величины Pi обладает весьма простыми свойствами. Он практически не
зависит от закона распределения СВ х, мало зависит от числа опытов n.
Он зависит от k. При увеличении R он
приближается к
, то при больших
значениях nзакон
распределения величины Pi обладает весьма простыми свойствами. Он практически не
зависит от закона распределения СВ х, мало зависит от числа опытов n.
Он зависит от k. При увеличении R он
приближается к ![]() .
.
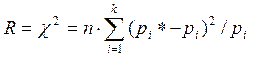 (4)
(4)
Поэтому
первое расхождение обычно называется ![]() . Учитывая, что
. Учитывая, что
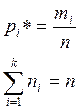 , то получим
, то получим ![]() (5)
(5)
Распределение ![]() зависит от числа степеней свободы d.
зависит от числа степеней свободы d.
В формуле 5 число степеней свободы равно числу k – число независимых условий.
1. сумма вероятности
равна 1: 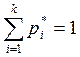 - всегда.
- всегда.
2. требование совпадения статистического среднего с
гипотетическим: 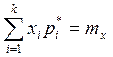
3. совпадение дисперсии: 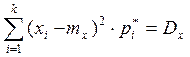
Для распределения ![]() составлены таблицы, по которым для каждого
значения
составлены таблицы, по которым для каждого
значения ![]() и числа степеней свободы можно найти
вероятность того, что случайная величина распределяется по закону
и числа степеней свободы можно найти
вероятность того, что случайная величина распределяется по закону ![]() .
.
Распределение ![]() дает возможность оценить расхождение между
гипотетическим распределением 2 и статистическим 1. Если вероятность очень
мала, то есть не превосходит выбранного нами уровня значимости
дает возможность оценить расхождение между
гипотетическим распределением 2 и статистическим 1. Если вероятность очень
мала, то есть не превосходит выбранного нами уровня значимости ![]() , то опытные данные противоречат гипотезе Н.
соответственно эту гипотезу надо отбросить. Если вероятность Р не мала,
то можно признать расхождение между распределениями 1 и 2 не существенными и
считать гипотезу Н правдоподобной (или не противоречащей опытным
данным).
, то опытные данные противоречат гипотезе Н.
соответственно эту гипотезу надо отбросить. Если вероятность Р не мала,
то можно признать расхождение между распределениями 1 и 2 не существенными и
считать гипотезу Н правдоподобной (или не противоречащей опытным
данным).
Пример:
Произведено
800 наблюдений над случайной величиной Х, которая может принимать
следующие значения: Х1 = 0, Х2 = 1, …, Х11 = 10. ![]()
В результате наблюдений получены следующие значения:
|
Хi |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
ni |
25 |
81 |
124 |
146 |
175 |
106 |
80 |
35 |
16 |
6 |
6 |
Требуется оценить
правдоподобие гипотезы Н, состоящее в том, что СВ распределена по закону
Пуассона параметром![]() равным статистическому среднему
наблюдаемому значению. В качестве уровня значимости принять
равным статистическому среднему
наблюдаемому значению. В качестве уровня значимости принять ![]() .
.
Решение:
Разделим
![]() на число опытов 800 и получим
статистический ряд:
на число опытов 800 и получим
статистический ряд:
|
Хi |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
0.031 |
0.101 |
0.155 |
0.183 |
0.219 |
0.132 |
0.1 |
0.044 |
0.02 |
0.008 |
0.008 |
Найдем
статистическое среднее ![]()
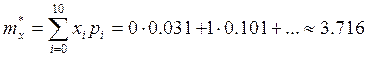
найдем вероятность ![]() ,
соответствующее закону Пуассона с параметрами
,
соответствующее закону Пуассона с параметрами ![]() =
=![]()
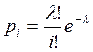
|
Хi |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Pi |
0.243 |
0.0904 |
0.168 |
0.208 |
0.193 |
0.144 |
0.089 |
0.047 |
0.022 |
0.0091 |
0.0033 |
По
формуле 5 находим значение ![]()
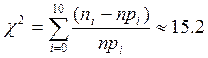
Число степеней свободы равно числу значений СВ минус 2 накладывается ограничение
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.