Ответы на экзаменационные вопросы № 1-30 дисциплины "Математические методы и модели" (Модели пластов и процессов разработки, типы моделей пластов. Основы методик построения моделей пластов по геолого-физическим промысловым данным)

Несколько событий называются совместными, если любые два из них при однократном наблюдении могут появиться вместе. Из приведенных выше событий совместными являются A, D, Е и F, или А, С и Е, или В, С и Е.

Два события называются несовместными, если их совместное появление невозможно. Так, среди названных событий несовме­стны А и В, С и D.

Суммой нескольких событий называется событие, когда в ре­зультате наблюдения появляется хотя бы одно из этих событий. Рассмотрим систему событий А₁,А_2, А₃, заключающихся в том, что скважина может вскрыть пласт, сложенный соответственно песчани­ком, алевролитом и аргиллитом. Тогда, например, сложное событие А = А₁ + А₂ есть событие, состоящее в том, что скважина вскроет пласт, представленный коллектором.

Произведением нескольких событий называется событие, когда все эти события в результате наблюдения появляются совместно. Если обратиться к рассмотренным ранее событиям А, В, С, D, E, F, то сложное событие G = ADEFозначает «пласт представлен песча­ником, насыщенным нефтью, имеющим пористость более 16% и нефтенасыщенность более 85%». События А₁, А ₂, . . ., А_п образуют полную группу событий, если в результате опыта хотя бы одно из них обязательно произойдет. Например, если породы, слагающие пласт, мы делим на три типа: песчаники, алевролиты и аргиллиты, то события А₁ — вскрытие скважиной песчаника, А₂ — вскрытие скважиной алевролита и А₃ — вскрытие скважиной аргиллита образуют полную группу, так как при бурении обязательно будет вскрыт какой-либо из этих типов пород.

Два несовместных события, образующих полную группу, назы­ваются противоположными. Событие, противоположное А, обозна­чается . Если А — вскрытие скважиной коллектора, то  — вскры­тие неколлектора.

Для решения практических задач важно уметь количественно оценивать величины вероятностей случайных событий. Как указы­валось, вероятность есть численная мера объективной возможности события. В понятие вероятности вкладывается определенный прак­тический смысл. На основании опыта считается, что более вероятны те события, которые происходят чаще. В связи с этим в настоящее время при определении понятия вероятности исходят из элементар­ного понятия относительной частоты события.

Существует еще один способ определения вероятности случайного события – геометрический.

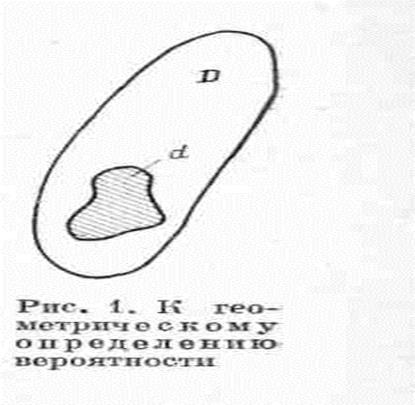
Пусть на плоскости имеется некоторая область D,площадь которой равна S_D, и в ней выделена друга область d, площадь которой S_d(рис. 1). В область Dслучайным образом попадает точка. Чему равна вероятность того, что она попадет в область d ?   

Предполагается, что точка может попасть в любую точку  области  D,   и   вероятность   попадания   в   какую-либо   часть   области  Dпропорциональна   площади   этой   части   и не   зависит   от   ее   формы и расположения. При этих условиях вероятность попадания случайно брошенной точки в область dравна  

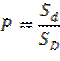
Таким образом, вероятность появления случайной точки внутри некоторой области определяется как отношение размера этой области к размеру всей области, в которой может появиться данная точка. Вероятность, определенная таким образом, называется геометри­ческой вероятностью. Одномерный и трехмерный случай (когда область Dесть отрезок линии или некоторый объем) отличаются от рассмотренного тем, что в них вместо площади нужно говорить о длинах и объемах.

В задачах нефтегазопромысловой геологии при вычислении геометрических вероятностей в качестве областей D и dмогут, например, рассматриваться соответственно: площадь залежи и суммарная площадь участков, на которых пласт имеет мощность (пористость, проницаемость) меньше некоторой каким-либо образом задан­ной величины или представлен коллекторами (неколлекторами); общая мощность пласта и суммарная мощность прослоев коллектора в отдельной